线性代数中的投影

投影矩阵的推导

假设我们想把一个向量 $\boldsymbol{b}$ 投影到线性空间 $\mathcal{S}$ 中，应该怎么做呢。

设投影后的向量为 $\boldsymbol{p}$ ，则有 $\boldsymbol{p}\in \mathcal{S}$ ，设误差向量（error vector） $\boldsymbol{e}=\boldsymbol{b}-\boldsymbol{p}$ ，则 $\boldsymbol{e}$ 应与 $\mathcal{S}$ 正交。投影就是将向量分为两部分 $\boldsymbol{b}=\boldsymbol{p}+\boldsymbol{e}$ ，一部分在 $\mathcal{S}$ 中，另一部分与 $\mathcal{S}$ 正交，然后取其中的 $\boldsymbol{p}$ 。也可以用图像直观理解：

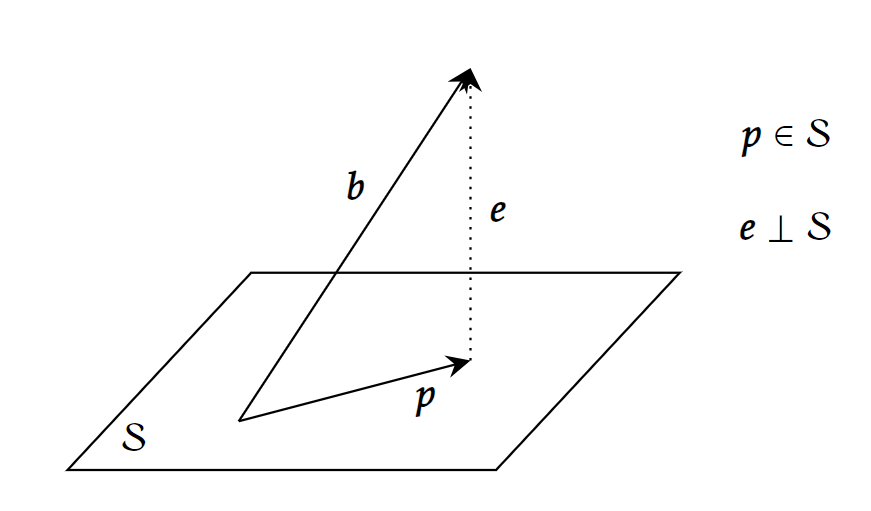
要求得 $\boldsymbol{p}$ ，只需要将 $\boldsymbol{p}\in \mathcal{S}\;\mathrm{(1)}$ 和 $\boldsymbol{e}\perp \mathcal{S}\;\mathrm{(2)}$ 这两个条件翻译成线性代数的语言即可。

首先，我们要先表达线性空间 $\mathcal{S}$ ，设 $\mathcal{S} \subset \mathbb{P}^m$ ， $\mathrm{dim}\mathcal{S}=n$ ，取 $\mathcal{S}$ 的一组基，作为矩阵 $A_{m\times n}$ 的列向量，则 $\mathcal{S}$ 就是 $A$ 的列空间， $\mathcal{S}=\mathrm{C}(A)$ 。

然后要翻译 $\boldsymbol{p}\in \mathcal{S}$ ，只需要令 $\boldsymbol{p}=A\hat{\boldsymbol{x}}$ ，其中 $\hat{\boldsymbol{x}}$ 为 $\mathbb{P}^m$ 中的任意向量。
翻译 $\boldsymbol{e}\perp\mathcal{S}$ ，就是 $\boldsymbol{e}\in\mathcal{S}^\perp=\mathrm{C}(A)^\perp=\mathrm{N}(A^T)$ ，即 $A^T\boldsymbol{e}=0$ 。

得到方程组

$\begin{cases} \boldsymbol{p}=A\hat{\boldsymbol{x}}\\ A^T\boldsymbol{e}=0 \end{cases}$

$\begin{align*} A^T \boldsymbol{e} &= 0 \\ A^T(\boldsymbol{b}-A\hat{\boldsymbol{x}}) &= 0 \\ A^T \boldsymbol{b} &= A^T A\hat{\boldsymbol{x}} \\ \hat{\boldsymbol{x}} &= (A^T A)^{-1}A^T\boldsymbol{b} \\ \boldsymbol{p} &= A(A^T A)^{-1}A^T\boldsymbol{b} \end{align*}$

令 $P=A(A^T A)^{-1}A^T$ ，称 $P$ 为 $\mathcal{S}$ 的投影矩阵（projection matrix），则要将 $\boldsymbol{b}$ 投影至 $\mathcal{S}$ ，只需左乘 $P$ 即可， $\boldsymbol{p}=P\boldsymbol{b}$ 。

这里的 $(A^T A)^{-1}$ 不能拆作 $A^{-1}(A^{-1})^T$ ，因为 $A$ 不一定为方阵，当 $n<m$ 时， $A$ 不可逆。当 $n=m$ 时， $A$ 必定可逆，因为列向量线性无关，然而当 $n=m$ 时，投影的意义不大，易得 $P=I$ ，投影不会改变任何东西。而 $(A^T A)^{-1}$ 一定是可逆的（想想为什么？）。

当 $A$ 是向量时

当 $A$ 是向量而非矩阵时，一切都没有变，我们仍然有 $\boldsymbol{p}=\boldsymbol{a}(\boldsymbol{a}^T \boldsymbol{a})^{-1} \boldsymbol{a}^T \boldsymbol{b}$ ，不过现在 $\boldsymbol{a}^T \boldsymbol{a}$ 是一个标量了，也可以写作

$\boldsymbol{p}=\frac{\boldsymbol{a}^T \boldsymbol{b}}{\boldsymbol{a}^T \boldsymbol{a}}\boldsymbol{a}=\frac{\boldsymbol{a}\cdot \boldsymbol{b}}{\boldsymbol{a}\cdot \boldsymbol{a}}\boldsymbol{a}$

这和我们常见的向量投影到另一个向量的形式是一致的。

投影矩阵的特性

1. 对称性

$P^T=P$

证明

$\begin{align*} P^T &= (A(A^T A)^{-1}A^T)^T \\ &= A((A^T A)^{-1})^T A^T \\ &= A((A^T A)^T)^{-1} A^T \\ &= A(A^T A)^{-1}A^T \\ &= P \end{align*}$

2. 幂等性

$P^k=P\quad(k=1,2,\dots)$

直观理解，就是将 $\boldsymbol{b}$ 投影到 $\mathcal{S}$ 后，再投影一次，没有任何变化，因为 $\boldsymbol{p}$ 已经在 $\mathcal{S}$ 里了。

证明

要证原命题，只需证 $P^2=P$

$\begin{align*} P^2 &= (A(A^T A)^{-1}A^T)(A(A^T A)^{-1}A^T) \\ &= A(A^T A)^{-1}(A^T A)(A^T A)^{-1}A^T \\ &= A(A^T A)^{-1}A^T \\ &= P \end{align*}$

两种极端情况

1. 当 $\boldsymbol{b}\in\mathcal{S}$ ，有 $P\boldsymbol{b}=\boldsymbol{b}$

已经在 $\mathcal{S}$ 上的向量再投影到 $\mathcal{S}$ 不会变化

证明

因为 $\boldsymbol{b}\in\mathrm{C}(A)$ ，则 $\exists\boldsymbol{x},\;s.t.\;\boldsymbol{b}=A\boldsymbol{x}$ ，有：

$\begin{align*} P\boldsymbol{b} &= A(A^T A)^{-1}A^TA\boldsymbol{x} \\ &= A(A^T A)^{-1}(A^T A)\boldsymbol{x} \\ &= A\boldsymbol{x} \\ &= \boldsymbol{b} \end{align*}$

2. 当 $\boldsymbol{b} \perp \mathcal{S}$ ，有 $P\boldsymbol{b}=0$

正交与 $\mathcal{S}$ 的向量，投影到 $\mathcal{S}$ 就只剩下一个点了

证明

$\boldsymbol{b}\perp\mathrm{C}(A) \Leftrightarrow \boldsymbol{b} \in \mathrm{N}(A^T)$ ，故 $A^T\boldsymbol{b}=0$

$\begin{align*} P\boldsymbol{b} &= A(A^T A)^{-1}A^T\boldsymbol{b} \\ &= A(A^T A)^{-1}(A^T\boldsymbol{b}) \\ &= 0 \end{align*}$

投影的应用

解一个无解的方程

$A\boldsymbol{x}=\boldsymbol{b}$ 有时是无解的，因为 $\boldsymbol{b}$ 不在 $A$ 的列空间 $\mathrm{C}(A)$ 中，于是我们可以将 $\boldsymbol{b}$ 投影到 $\mathrm{C}(A)$ 中。设 $\boldsymbol{p}$ 为 $\boldsymbol{b}$ 在 $\mathrm{C}(A)$ 的投影，则 $A\hat{\boldsymbol{x}}=\boldsymbol{p}$ 一定有解。

注意：这里的 $\boldsymbol{p}$ 不能和前文一样使用 $A(A^T A)^{-1}A^T\boldsymbol{b}$ 求得，因为前面的 $A$ 是列线性无关的，这里不一定。当 $A$ 列线性无关时， $\hat{\boldsymbol{x}}$ 有唯一解，当 $A$ 列线性相关时， $\hat{\boldsymbol{x}}$ 有无穷多解，无论如何， $\hat{\boldsymbol{x}}$ 总是存在的。

回归正题，我们解出来的这个 $\hat{\boldsymbol{x}}$ 虽然不是一个精确的解，但却是一个最好的解，这个 $\hat{\boldsymbol{x}}$ 可以令 $||A\boldsymbol{x}-\boldsymbol{b}||^2$ 最小，这一点可以从两个角度证明：

几何直观理解： $||A\boldsymbol{x}-\boldsymbol{b}||^2$ 就是 $A\boldsymbol{x}$ 和 $\boldsymbol{b}$ 的欧氏距离，所有可能的 $A\boldsymbol{x}$ 都在 $\mathrm{C}(A)$ 中，而 $\mathrm{C}(A)$ 中距离 $\boldsymbol{b}$ 最近的那个点，就是 $\boldsymbol{b}$ 的投影 $\boldsymbol{p}$ ，此时 $\boldsymbol{x}=\hat{\boldsymbol{x}}$ 。
代数严格证明：由 $||A\boldsymbol{x}-\boldsymbol{b}||^2=||A\boldsymbol{x}-\boldsymbol{p}-\boldsymbol{e}||^2=||A\boldsymbol{x}-\boldsymbol{p}||^2+||\boldsymbol{e}||^2\geq||\boldsymbol{e}||^2$ ，其中 $||\boldsymbol{e}||^2$ 是与 $\boldsymbol{x}$ 无关的常量，则当 $||A\boldsymbol{x}-\boldsymbol{p}||^2=0$ 时，取得最小值，此时 $A\boldsymbol{x}=\boldsymbol{p}$ ，即 $\boldsymbol{x}=\hat{\boldsymbol{x}}$

新的方程 $A\hat{\boldsymbol{x}}=\boldsymbol{p}$ ，不仅有“一定有解”、“解是最好的”这两个良好的性质，当 $A\boldsymbol{x}=\boldsymbol{b}$ 本身就有解时，新的方程与原方程的解是一致的，这是因为当 $\boldsymbol{b}\in\mathrm{C}(A)$ 时， $\boldsymbol{p}=\boldsymbol{b}$ （上面两种极端情况的第一种）。

也就是说，无论 $A\boldsymbol{x}=\boldsymbol{b}$ 是否有解，你可以不管三七二十一，就计算 $A\hat{\boldsymbol{x}}=\boldsymbol{p}$ ，肯定能解出来一个最好的 $\hat{\boldsymbol{x}}$ ，它满足“如果有精确解，我就是精确解，如果没有精确解，我就是最好的解”。你可以在对 $A$ 一无所知的情况下，保证能解出一个优秀的 $\hat{\boldsymbol{x}}$ 。

换一个形式

为了方便，下面还是假设 $A$ 列满秩。

$A\hat{\boldsymbol{x}}=\boldsymbol{p}=A(A^T A)^{-1}A^T\boldsymbol{b}$ ，我们都知道求逆矩阵既困难又会造成精度问题（浮点数计算时），于是可以两边都左乘 $A^T$ ，变成

$\begin{align*} A^T A\hat{\boldsymbol{x}}&=(A^T A)(A^T A)^{-1}A^T\boldsymbol{b} \\ A^T A\hat{\boldsymbol{x}}&=A^T\boldsymbol{b} \tag{1} \\ \hat{\boldsymbol{x}}&= (A^T A)^{-1}A^T\boldsymbol{b} \tag{2} \end{align*}$

其中 $\text{(1)}$ 是比较好用的形式

而 $\text{(2)}$ 在线性回归领域也写作

$\boldsymbol{\theta}=(X^T X)^{-1}X^T\boldsymbol{y}$

并被称为normal equation（或许译作正交方程？）

最小二乘法

最小二乘法其实可以从投影的角度理解，个人认为这是最巧妙，无需计算的解法了（相比于对均方误差求导的解法）

假设我们有 $m$ 个点 $(t_1,b_1),(t_2,b_2),\dots,(t_m,b_m)$ ，要找一条直线 $y=cx+d$ ，最佳拟合它们，即令 $\sum (ct_i+d-b_i)^2$ （也被称为均方误差，mean square error, MSE）最小。

只需令

$\boldsymbol{b}=\left[ \begin{array}{ll} b_1 \\ b_2 \\ \vdots \\ b_m \end{array}\right]\qquad A=\left[ \begin{array}{ll} 1 & t_1 \\ 1 & t_2 \\ \vdots & \vdots \\ 1 & t_m \end{array}\right]\qquad \boldsymbol{x}=\left[ \begin{array}{ll} d \\ c \end{array}\right]$

就有 $A\boldsymbol{x}=\boldsymbol{b}$ 。假如 $m$ 个点落在同一条直线上，这个方程才有解，大多数情况下，它是无解的，运用前面推导的式子，有

$A^T A=\left[\begin{array}{ll} m & \sum t_i \\ \sum t_i & \sum t_i^2 \end{array}\right]\qquad A^T \boldsymbol{b}=\left[\begin{array}{l} \sum b_i \\ \sum b_i t_i \end{array}\right]$

只需解

$\left[\begin{array}{ll} m & \sum t_i \\ \sum t_i & \sum t_i^2 \end{array}\right]\left[\begin{array}{l}d\\ c\end{array}\right]=\left[\begin{array}{l} \sum b_i \\ \sum b_i t_i \end{array}\right]$

即可得到使MSE最小的 $c$ 和 $d$ 。

拟合抛物线

假如将拟合直线变成拟合抛物线 $y=c_2x^2+c_1x+c_0$ ，只需要改成

$\boldsymbol{b}=\left[ \begin{array}{ll} b_1 \\ b_2 \\ \vdots \\ b_m \end{array}\right]\qquad A=\left[ \begin{array}{lll} 1 & t_1 & t_1^2 \\ 1 & t_2 & t_2^2 \\ \vdots & \vdots & \vdots \\ 1 & t_m & t_m^2 \end{array}\right]\qquad \boldsymbol{x}=\left[ \begin{array}{ll} c_0 \\ c_1 \\ c_2 \\ \end{array}\right]$