谱定理（Spectral Theorem）的证明

回顾特征值分解/对角化

定义

对于 $n \times n$ 的方阵 $\boldsymbol{A}$ ，如果有下面的等式：

$\boldsymbol{Ax}=\lambda \boldsymbol{x}$

其中 $\boldsymbol{x}$ 为非零向量。

我们就称 $\boldsymbol{x}$ 是 $\boldsymbol{x}$ 的一个特征向量（eigenvector）， $\lambda$ 是 $\boldsymbol{x}$ 的一个特征值（eigenvalue）。

求解

$\begin{align*} \boldsymbol{Ax} &= \lambda \boldsymbol{Ix} \\ (\boldsymbol{A} - \lambda \boldsymbol{I})\boldsymbol{x} &= \boldsymbol{0} \\ \det(\boldsymbol{A} - \lambda \boldsymbol{I}) &= 0 \\ \end{align*}$

特征值可以通过解特征根方程 $\det(\boldsymbol{A}-\lambda \boldsymbol{I})=0$ 来求得。由代数基本定理，这个多项式方程一定有 $n$ 个复根（可能有重根）

由于行列式为0， $(\boldsymbol{A}-\lambda \boldsymbol{I})\boldsymbol{x}=\boldsymbol{0}$ 一定有非零解，任取一非零解，即可得出特征向量 $\boldsymbol{x}$ 。

如果 $\boldsymbol{A}$ 有 $n$ 个线性无关的特征向量 $\boldsymbol{x}_1, \boldsymbol{x}_2, \dots, \boldsymbol{x}_n$ ，对应的 $n$ 个特征值为 $\lambda_1, \lambda_2, \dots, \lambda_n$ ，令 $\boldsymbol{X}=(\boldsymbol{x}_1, \boldsymbol{x}_2, \dots, \boldsymbol{x}_n)$ ， $\boldsymbol{\Lambda}=\mathrm{diag}(\lambda_1, \lambda_2, \dots, \lambda_n)$ 则

$\begin{align*} \boldsymbol{AX}&=\boldsymbol{X \Lambda} \\ \boldsymbol{A}&=\boldsymbol{X \Lambda} \boldsymbol{X}^{-1} \tag{1} \end{align*}$

$(1)$ 式称作 $\boldsymbol{A}$ 的特征值分解，此时 $\boldsymbol{A}$ 称作可对角化（diagonalizable）。

实对称矩阵 $\boldsymbol{S}$ 必定可对角化，且一定可以选取两两正交的的单位特征向量，使得 $\boldsymbol{X}$ 为正交矩阵 $\boldsymbol{Q}$ ，这时原式可以写成这样。

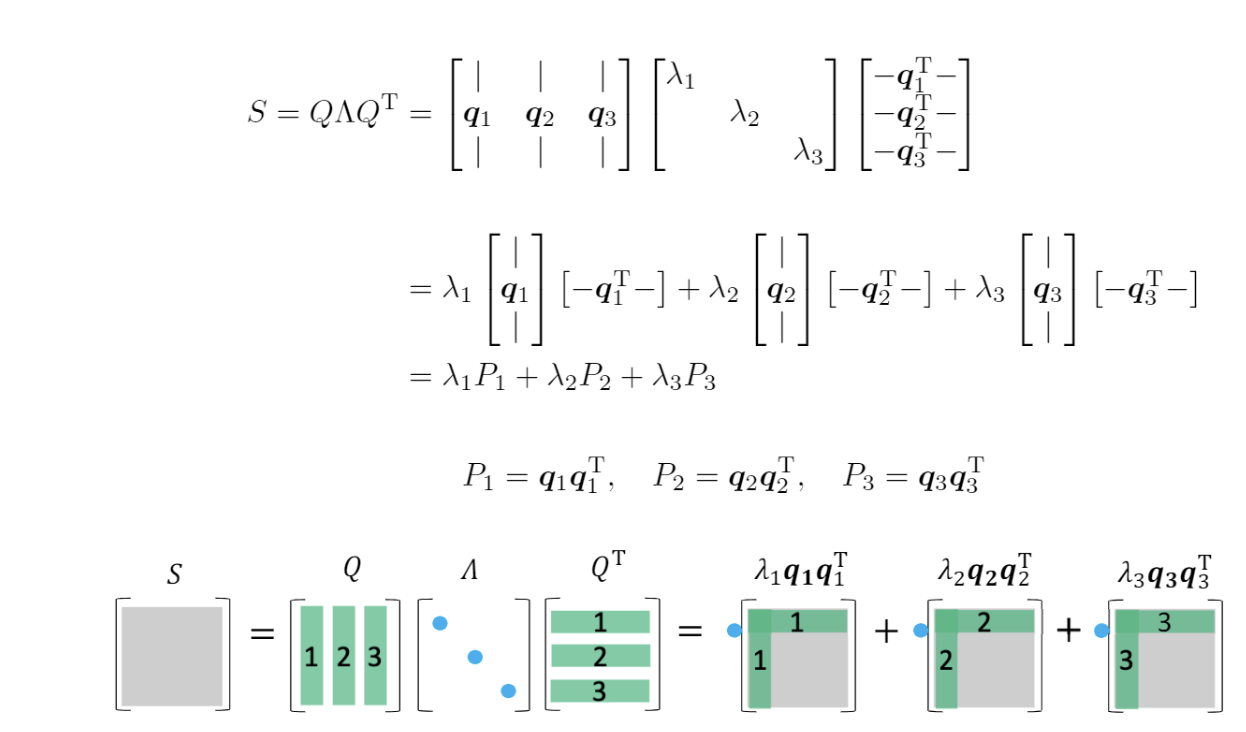
图来自Github仓库The-Art-of-Linear-Algebra

下面，我们将要把实对称矩阵推广到所有正规矩阵，将正交矩阵推广到复数域的酉矩阵。

通向SVD的基础：谱定理

定义：对称矩阵

若 $\boldsymbol{A}=\boldsymbol{A}^*$ ，称 $\boldsymbol{A}$ 为对称矩阵（symmetric matrix）。
这里的 $\boldsymbol{A}^*=\overline{\boldsymbol{A}}^\mathrm{T}$ ，表示 $\boldsymbol{A}$ 的共轭转置（conjugate transpose）。

定义：酉矩阵

若 $\boldsymbol{U}^*\boldsymbol{U}=\boldsymbol{UU}^*=\boldsymbol{I}$ ，称方阵 $\boldsymbol{U}$ 为酉矩阵（unitary matrix）

推论 $\boldsymbol{U}^* = \boldsymbol{U}^{-1}$

定义：正规矩阵

若 $\boldsymbol{A}\boldsymbol{A}^*=\boldsymbol{A}^* \boldsymbol{A}$ ，称方阵 $\boldsymbol{A}$ 为正规矩阵（normal matrix）。

显然，对称矩阵和酉矩阵都是正规矩阵

谱定理（Spectral Theorem）

谱定理在线性代数里可以这样表述

$\boldsymbol{A}$ 是正规矩阵当且仅当存在酉矩阵 $\boldsymbol{U}$ ，使得

$\boldsymbol{A}=\boldsymbol{U \Lambda U}^* \tag{2}$

其中 $\boldsymbol{\Lambda}$ 为对角阵。

结合特征值分解和酉矩阵的定义，不难发现 $(2)$ 其实就是一种特殊的特征值分解 $\boldsymbol{A}=\boldsymbol{U \Lambda U}^{-1}$ ， $\boldsymbol{\Lambda}$ 就是特征值组成的对角阵 $\boldsymbol{\Lambda}=\mathrm{diag}(\lambda_1, \lambda_2, \dots, \lambda_n)$ 。

证明

必要性

$\begin{align*} \boldsymbol{A} &= \boldsymbol{U \Lambda U}^* \\ \boldsymbol{AA}^* &= \boldsymbol{U \Lambda U}^* \boldsymbol{U} \overline{\boldsymbol{\Lambda}}\boldsymbol{U}^* \\ &= \boldsymbol{U \Lambda \overline{\Lambda} U}^* \\ \boldsymbol{A}^*\boldsymbol{A} &= \boldsymbol{U \overline{\Lambda} U}^* \boldsymbol{U} \boldsymbol{\Lambda}\boldsymbol{U}^* \\ &= \boldsymbol{U \overline{\Lambda} \Lambda U}^* \\ \end{align*}$

其中 $\boldsymbol{\Lambda \overline{\Lambda}}=\boldsymbol{\overline{\Lambda} \Lambda}=\mathrm{diag}(|\lambda_1|^2, |\lambda_2|^2, \dots, |\lambda_n|^2)$ 。故 $\boldsymbol{AA}^*=\boldsymbol{A}^*\boldsymbol{A}$ ， $\boldsymbol{A}$ 为正规矩阵。

充分性

使用数学归纳法，当 $n=1$ ，结论显然成立。若谱定理对 $n-1$ 成立，下面证明其对 $n$ 成立。

任取特征值 $\lambda_1$ ，和对应的特征向量 $\boldsymbol{x}_1$ （存在至少一个，一定能取到！），标准化这个特征向量 $\boldsymbol{q}=\frac{\boldsymbol{x}_1}{|\boldsymbol{x}_1|}$ ，则 $\boldsymbol{q}^*\boldsymbol{q}=1$ 。

$\begin{align*} \boldsymbol{Aq}&=\lambda_1\boldsymbol{q} \\ \boldsymbol{q}^*\boldsymbol{Aq}&=\lambda_1\boldsymbol{q}^*\boldsymbol{q}=\lambda_1 \\ \end{align*}$

任取一组包含 $\boldsymbol{q}$ 的基，经过Gram-Schmidt 正交化，和标准化，得到酉矩阵 $(\boldsymbol{q}, \boldsymbol{q}_2, \dots, \boldsymbol{q}_n)=(\boldsymbol{q}, \boldsymbol{Q})$

则

$\begin{align*} \boldsymbol{q}^*\boldsymbol{Q} = \boldsymbol{Q}^* \boldsymbol{q} &= 0 \tag{3} \\ \boldsymbol{Q}^* \boldsymbol{Q} &= \boldsymbol{I} \tag{4} \end{align*}$

为了对 $\boldsymbol{Q}^*\boldsymbol{AQ}$ 应用谱定理，需要证明 $\boldsymbol{Q}^*\boldsymbol{AQ}$ 为正规矩阵。

$\begin{align*} (\boldsymbol{Q}^*\boldsymbol{AQ})(\boldsymbol{Q}^*\boldsymbol{AQ})^* &= \boldsymbol{Q}^* \boldsymbol{AA}^* \boldsymbol{Q} \\ (\boldsymbol{Q}^*\boldsymbol{AQ})^*(\boldsymbol{Q}^*\boldsymbol{AQ}) &= \boldsymbol{Q}^* \boldsymbol{A}^*\boldsymbol{A} \boldsymbol{Q} \\ \end{align*}$

由 $\boldsymbol{A}$ 正规 $\boldsymbol{AA}^* = \boldsymbol{A}^* \boldsymbol{A}$ ，得 $\boldsymbol{Q}^*\boldsymbol{AQ}$ 正规。

由谱定理对于 $n-1$ 成立，应用 $(2)$ 式，有

$\boldsymbol{Q}^* \boldsymbol{A} \boldsymbol{Q} = \boldsymbol{V} \boldsymbol{\Lambda}_1 \boldsymbol{V}^* \tag{5}$

其中 $\boldsymbol{\Lambda}_1,\boldsymbol{V}$ 均符合谱定理的描述的性质。

令

$\boldsymbol{U} = \left(\begin{array}{c} \boldsymbol{q} & \boldsymbol{QV} \\ \end{array}\right)$

根据 $(3),(4)$

$\boldsymbol{U}^*\boldsymbol{U} = \left( \begin{array}{c} \boldsymbol{q}^*\boldsymbol{q} & \boldsymbol{q}^* \boldsymbol{Q} \boldsymbol{V} \\ \boldsymbol{V}^* \boldsymbol{Q}^* \boldsymbol{q} & \boldsymbol{V}^* \boldsymbol{Q}^* \boldsymbol{Q} \boldsymbol{V} \\ \end{array} \right)=\boldsymbol{I}$

故 $\boldsymbol{U}$ 是酉矩阵

$\begin{align*} \boldsymbol{U}^* \boldsymbol{A} \boldsymbol{U} &= \left(\begin{array}{c} \boldsymbol{q}^* \boldsymbol{A} \boldsymbol{q} & \boldsymbol{q}^* \boldsymbol{A} \boldsymbol{Q} \boldsymbol{V} \\ \boldsymbol{V}^* \boldsymbol{Q}^* \boldsymbol{A} \boldsymbol{q} & \boldsymbol{V}^* \boldsymbol{Q}^* \boldsymbol{A} \boldsymbol{Q} \boldsymbol{V} \end{array}\right) \end{align*}$

根据 $(5)$ 有

$\begin{align*} \boldsymbol{AQV} &= \boldsymbol{QV\Lambda}_1 \\ \boldsymbol{V}^* \boldsymbol{Q}^* \boldsymbol{A} &= \boldsymbol{\Lambda}_1 \boldsymbol{V}^* \boldsymbol{Q}^* \\ \boldsymbol{V}^* \boldsymbol{Q}^* \boldsymbol{AQV} &= \boldsymbol{\Lambda}_1 \end{align*}$

则

$\begin{align*} \boldsymbol{U}^*\boldsymbol{AU} &= \left(\begin{array}{c} \lambda_1 \boldsymbol{q}^* \boldsymbol{q} & \boldsymbol{q}^* \boldsymbol{QV\Lambda}_1 \\ \boldsymbol{\Lambda}_1 \boldsymbol{V}^* \boldsymbol{Q}^* \boldsymbol{q} & \boldsymbol{\Lambda}_1 \end{array}\right)\\ &= \left(\begin{array}{c} \lambda_1 & \\ & \boldsymbol{\Lambda}_1 \\ \end{array}\right) \\ &= \boldsymbol{\Lambda} \end{align*}$