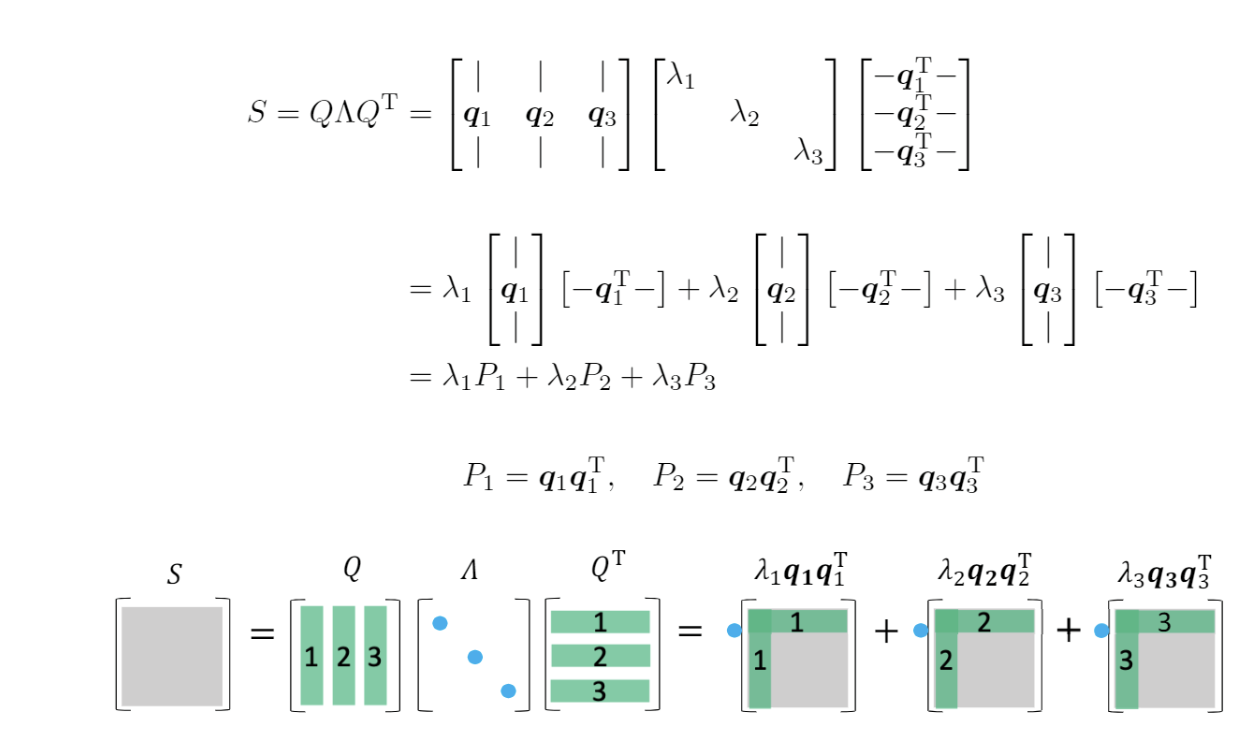
线性空间到底是什么？能不能用一句话定义线性空间？为什么线性空间一定有基？

线性空间到底是什么？

我们在学习线性代数的时候，通常见到的线性空间是由以下八个条件共同定义的：

设 $K$ 是一个数域， $V$ 是一个非空集合，同时还定义了：

向量加法： $+: V \times V \rightarrow V$
标量乘法： $\cdot: K \times V \rightarrow V$ （ $\cdot$ 也可省略）

且两种运算满足以下八条：

则成 $V$ 是定义在 $K$ 上的线性空间，又称向量空间。

向量加法单位元存在：存在 $\theta \in K$ 使得 $\alpha + \theta = \alpha, \quad \alpha \in V$ ，称 $\theta$ 为 $K$ 的零元素，即向量加法的单位元。
向量加法逆元存在：存在 $\forall \alpha \in V, \exists \beta \in V$ 使得 $\alpha + \beta = \theta$ ，称 $\beta$ 为 $V$ 的负元素，即向量加法的逆元。
向量加法结合律： $(\alpha + \beta) + \gamma = \alpha + (\beta + \gamma), \quad \alpha, \beta, \gamma \in V$
向量加法交换律： $\alpha + \beta = \beta + \alpha, \quad \alpha, \beta \in V$
标量乘法单位元存在：存在 $1 \in K$ 使得 $1 \cdot \alpha = \alpha, \quad \alpha \in V$ ，称 $1$ 为 $K$ 的单位元，即标量乘法的单位元。
标量乘法对向量加法的分配律： $c \cdot (\alpha + \beta) = c \cdot \alpha + c \cdot \beta, \quad c \in K, \alpha, \beta \in V$
标量乘法对域加法的分配律： $(c_1 + c_2) \cdot \alpha = c_1 \cdot \alpha + c_2 \cdot \alpha, \quad c_1, c_2 \in K, \alpha \in V$
标量乘法与域乘法的结合律： $(c_1 c_2) \cdot \alpha = c_1 (c_2 \cdot \alpha), \quad c_1, c_2 \in K, \alpha \in V$

整整八条，实在劝退，有没有更简单的方式来表达这些呢？

维基百科上对线性空间的概括定义是

$(K, +, \times)$ 是一个域，且 $V$ 是一个 $K-$ 模。

本文将从八个条件出发，根据抽象代数中域和模的定义，来解释这一句话。前半部分亦可作为抽象代数中基本概念的速览。

群、环、域、模

群

群是指一个集合 $G$ ，和一个运算 $\circ: G \times G \rightarrow G$ （封闭性），满足以下条件：

结合律： $\forall a, b, c \in G, (a \circ b) \circ c = a \circ (b \circ c)$
单位元：存在 $e \in G$ ，使得 $\forall a \in G, e \circ a = a$ ，称 $e$ 为群的单位元（Identity），又称幺元。
逆元：对任意 $a \in G$ ，存在 $a^{-1} \in G$ ，使得 $a^{-1} \circ a = e$ ，称 $a^{-1}$ 为 $a$ 的逆元（Inverse）。

就称 $(G, \circ)$ 为一个群（Group）。需要注意的是，群不一定满足交换律，在群的定义的基础上，由满足交换律 $a \circ b = b \circ a$ 的群称为交换群，又叫Abel群。

群的例子：

$(\mathbb{Z}, +)$ ，整数关于加法满足结合律、单位元 $0$ 存在、逆元 $-a$ 存在，构成一个群，不仅如此，这还是一个交换群。
$(\mathbb{R}-\{0\}, \times)$ ，去掉零的实数关于乘法满足结合律、单位元 $1$ 存在、逆元 $a^{-1}$ 存在，构成一个群，也是一个交换群。
非交换群的一个例子：六阶二面体群

我们可以看出，线性空间定义的前4条，现在可以用一句话概括：

$(V, +)$ 是一个交换群。

比群更简单的结构

上面群的定义可以概括成封闭性、结合律、单位元、逆元四个条件，可以进一步分解为：

满足封闭性就可以称为原群（Magma）
满足封闭性、结合律就可以称为半群（Semigroup）
满足封闭性、结合律、单位元就可以称为幺半群（Monoid）

环

不同地方对环的定义存在分歧，最常见的定义是以下这种

若 $(R, +, \times)$ 满足：

$(R, +)$ 是一个交换群
$(R, \times)$ 是一个幺半群
左分配律： $a(b + c) = ab + ac$
右分配律： $(b + c)a = ba + ca$

则称 $(R, +, \times)$ 为一个环（Ring）。

环不一定满足乘法交换律，满足乘法交换律的环叫做交换环。

环的例子：

$(\mathbb{Z}, +, \times)$ ，是环。
实系数矩阵 $M_n(\mathbb{R})$ 是环。
有理系数多项式 $\mathbb{Q}[x]$ 是环。

除环

如果任何环中的非零元都存在乘法逆元，即：

$\forall a \in R\backslash\{0\}, \exists a^{-1} \in R\backslash\{0\}$ ，使得 $a^{-1} \cdot a = 1$ ，则称 $(R, +, \times)$ 为一个除环。

域

交换的除环就是域（Field）。

$\mathbb{Q}$ 、 $\mathbb{R}$ 、 $\mathbb{C}$ 都是域。但是 $\mathbb{Z}$ 不是域，因为 $\mathbb{Z}$ 中只有 $1, -1$ 两个元素存在乘法逆元。

模

若 $R$ 是一个环， $1_R$ 是环的幺元， $(M, +)$ 构成一个交换群，且有一个运算 $\cdot: R \times M \rightarrow M$ ，称为标量乘法。

若这个标量乘法对所有 $r, s \in R$ , $x, y \in M$ ，满足：

$(r \cdot s) \cdot x = r \cdot (s \cdot x)$
$r \cdot (x + y) = r \cdot x + r \cdot y$
$(r + s) \cdot x = r \cdot x + s \cdot x$
$1_R \cdot x = x$

则称 $M$ 是一个左 $R-$ 模。

若基于上面的定义，但交换标量乘法的运算顺序，则称 $M$ 是一个右 $R-$ 模。

线性空间的定义

到模这一步就已经很抽象了，恭喜你坚持到了这里，现在我们终于可以定义线性空间了：

$(K, +, \times)$ 是一个域，且 $V$ 是一个 $K-$ 模。

线性空间的八条定义里，前四条实际上规定了 $(V, +)$ 是一个交换群，而后四条正好就是模的定义中的四条。因此说 $V$ 是一个 $K-$ 模，这就是定义的后半句话。

那么，这个定义中的前半句话可不可以去掉呢？模的定义里已经要求 $K$ 是一个环了，但是线性空间这里，把环的这个条件加强到了域，这有必要吗？

为什么线性空间要定义在域上？

我们这里不去讨论这样定义的历史原因，而是去讨论其合理性。

这非常有必要，因为这个条件保证了线性空间存在基。熟悉线性代数的朋友都应该非常清楚，基是线性代数中非常重要的概念，没有了基，线性代数中很多定理都无法成立。线性空间优良的性质也不存在了。

要理解这个定义，我们首先要证明这个定义下，线性空间一定有基，而且这个证明需要用到 $K$ 是一个域的这个条件。

证明线性空间一定有基

我们学习线性代数的时候，通常讨论的是有限维线性空间，证明有限维线性空间存在基比较简单，并且不需要用到Zorn引理，此处为了证明的泛用性，我们的证明将涵盖无穷维线性空间。

Hamel基

基有多种不同的定义，此处指的是最常用的Hamel基。Hamel基的定义如下：

设 $V$ 为一向量空间，Hamel基是指一组向量组 $H \subset V$ ，满足：

$H$ 线性无关，即：
任取 $H$ 中有限个向量 $\alpha_1, \alpha_2, \cdots, \alpha_n \in H$ ，则 $\sum_{i=1}^n c_i \alpha_i = 0$ 当且仅当 $c_1 = c_2 = \cdots = c_n = 0$ 。
（注意此处加粗的“有限个”很重要）
$H$ 可以张成整个 $V$ ， $\mathop{\mathrm{span}} H = V$ ，即：
$V = \left\{ \sum c_i \alpha_i : c_i \in K, \, \alpha_i\in H \right\}$ 。

存在性证明

定理：任何线性空间都有Hamel基

或者更进一步的，任何线性无关向量组都可以扩展出一组基：

定义：设 $S$ 是线性空间 $V$ 中的线性无关向量组，则存在Hamel基 $H \supset S$ 。

证明需要用到Zorn引理：

Zorn引理：设 $\mathscr{S}$ 为一非空偏序集，若 $\mathscr{S}$ 中任意全序集都在 $\mathscr{S}$ 中存在上界，则 $\mathscr{S}$ 中必有极大元。

设 $\mathscr{S}$ 为 $V$ 中所有包含 $S$ 的线性无关向量组的集合， $(\mathscr{S}, \subset)$ 构成一偏序集，显然 $\mathscr{S}$ 非空，设 $\mathscr{S}_0 \in \mathscr{S}$ 为一全序子集，则令 $X = \bigcup_{S_i \in \mathscr{S}_0} S_i$ ，有：

$X$ 是 $\mathscr{S}_0$ 的上界：显然。
$X \in \mathscr{S}$ ，只需证明 $X$ 线性无关。

下证 $X$ 线性无关：

由 $S_i$ 构成全序集，知可以令 $S_1 \subset S_2 \subset S_3 \subset \cdots$ 。

任取有限个向量 $\alpha_1, \alpha_2, \cdots, \alpha_n \in X$ ，则由于 $X = \bigcup_{S_i \in \mathscr{S}_0} S_i$ ，对任意 $\alpha_i$ ，存在 $j_i$ ， $\alpha_i \in S_{j_i}$ 。令 $j = \max\{j_1, j_2, \cdots, j_n\}$ ，则 $\forall i, \alpha_i \in S_j$ 。又因为 $\alpha_i \in S_j \in \mathscr{S}$ ， $\alpha_i$ 构成的向量组线性无关。 $\alpha_i$ 可以任取，由线性无关定义， $X$ 线性无关， $X \subset \mathscr{S}$ 。

由 $X$ 是 $\mathscr{S}_0$ 的上界和 $X \subset \mathscr{S}$ ，应用佐恩引理， $\mathscr{S}$ 中必有极大元，设 $H$ 为一极大元，则 $H \supset S$ 且 $H$ 线性无关。

考察Hamel基的定义，线性无关已满足，还需证明 $H$ 可以张成 $V$ 。任取 $x \in V$ ，则 $H \cup \{x\}$ 一定线性相关。因为若线性无关，设 $H' = H \cup \{x\}$ ，则 $H' \supset H$ 且 $H' \in \mathscr{S}$ ，这与 $H$ 是极大元矛盾。

由 $H$ 线性无关， $H'$ 也线性无关，知存在不全为零的 $c_1, c_2, \cdots, c_n$ ，和 $c_{n+1} \neq 0$ ，使得 $c_1 \alpha_1 + c_2 \alpha_2 + \cdots + c_n \alpha_n + c_{n+1} x = 0$ 。

则 $x = c_{n+1}^{-1} (c_1 \alpha_1 + c_2 \alpha_2 + \cdots + c_n \alpha_n)$ ，即任意 $x \in V$ 均可被 $H$ 线性表示， $\mathop{\mathrm{span}} H = V$ 。

综上得证。

模不一定有基

回到我们原来的问题来，为什么线性空间一定要定义在域上？这是因为一般的模不一定存在基，存在基的模叫做自由模（Free Basis）我们有：

除环上的模必为自由模。

考察我们上面的证明，最后一部中用到了 $c_{n+1}^{-1}$ ，这一步就要求了 $K$ 中存在乘法逆元，而模并不能保证这一点。

为了方便理解，下面举一个不存在基的模的例子。这个模就是 $\mathbb{Z}-$ 模 $\mathbb{Q}$ 。

证明 $\mathbb{Z}-$ 模 $\mathbb{Q}$ 不存在基：

设这个模为 $M$ 。首先，我们有任意两个非零元素都线性相关， $\forall p, q \in \mathbb{Q}\backslash \{0\}$ ，存在 $x, y \in \mathbb{Z}$ ，使得 $xp + yq = 0$ ，这是显然的。

因此如果 $M$ 有基 $B$ ，一定有 $|B| = 1$ ，设一个基为 $B = \{f\}, f \in \mathbb{Q}\backslash\{0\}$ ，则 $\mathop{\mathrm{span}} B = \{0, \pm f, \pm 2 f, \cdots\}$ 。显然 $f / 2 \in M，f / 2 \notin \mathop{\mathrm{span}} B$ 。故这个基不能张成 $M$ ，矛盾。

基在线性空间中的作用

想到哪写到哪，早就偏题了，思绪比较混乱，望谅解。

为什么基这么重要，因为对于任何一个数学结构，只要能够证明他是一个线性空间，那么就可以取一组基，然后你就获得了整个线性代数，可以使用线性代数中熟悉的概念。而在群/环/模论中，不同的群/环/模可能有截然不同的性质，没办法这样通用地去研究。

例如在Hilbert空间里，傅里叶变换就是将函数变换到一组特殊的正交基上

定义内积

$\langle\alpha, \beta\rangle = \lim_{T \to \infty} \frac{1}{T} \int_{-T/2}^{+T/2} \alpha(t) \overline{\beta}(t) \mathrm{d}t$

选取正交基 $e^{i 2 \pi f t}$

不难发现这组基是正交的：

$\langle e^{i 2 \pi f_1 t}, e^{i 2 \pi f_2 t}\rangle = \begin{cases} 1 & f_1 = f_2 \\ 0 & f_1 \neq f_2 \end{cases}$

在此基础上我们就可以推出傅里叶变换：

把信号 $x(t)$ 用正交基 $e^{i 2 \pi f_n t}$ 表示为：

$\begin{align*} x(t) &= \lim_{T \to \infty} \sum_{n = -\infty}^{\infty} \langle x, e^{i 2 \pi f_n t} \rangle e^{i 2 \pi f_n t}\\ &= \lim_{T \to \infty} \sum_{n = -\infty}^{\infty} \frac{1}{T} \int_{-T/2}^{+T/2} x(t) e^{-i 2 \pi f_n t}\mathrm{d}t \cdot e^{i 2 \pi f_n t}\\ \end{align*}$

其中 $f_n = \frac{n}{T}$ 。 $\Delta f = \frac{1}{T}$ ，所以上式可以写成：

$\begin{align*} x(t) &= \lim_{T \to \infty} \sum_{n = -\infty}^{\infty} \Delta f \int_{-T/2}^{+T/2} x(t) e^{-i 2 \pi f_n t}\mathrm{d}t \cdot e^{i 2 \pi f_n t}\\ &= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} x(t) e^{-i 2 \pi f t} \mathrm{d}t \cdot e^{i 2 \pi f t} \mathrm{d}f\\ \end{align*}$