回顾特征值分解/对角化
定义
对于n×n的方阵A,如果有下面的等式:
Ax=λx
其中x为非零向量。
我们就称x是x的一个特征向量(eigenvector),λ是x的一个特征值(eigenvalue)。
求解
Ax(A−λI)xdet(A−λI)=λIx=0=0
特征值可以通过解特征根方程det(A−λI)=0来求得。 由代数基本定理,这个多项式方程一定有n个复根(可能有重根)
由于行列式为0,(A−λI)x=0一定有非零解,任取一非零解,即可得出特征向量x。
如果A有n个线性无关的特征向量x1,x2,…,xn,对应的n个特征值为λ1,λ2,…,λn,令X=(x1,x2,…,xn),Λ=diag(λ1,λ2,…,λn)则
AXA=XΛ=XΛX−1(1)
(1)式称作A的特征值分解,此时A称作可对角化(diagonalizable)。
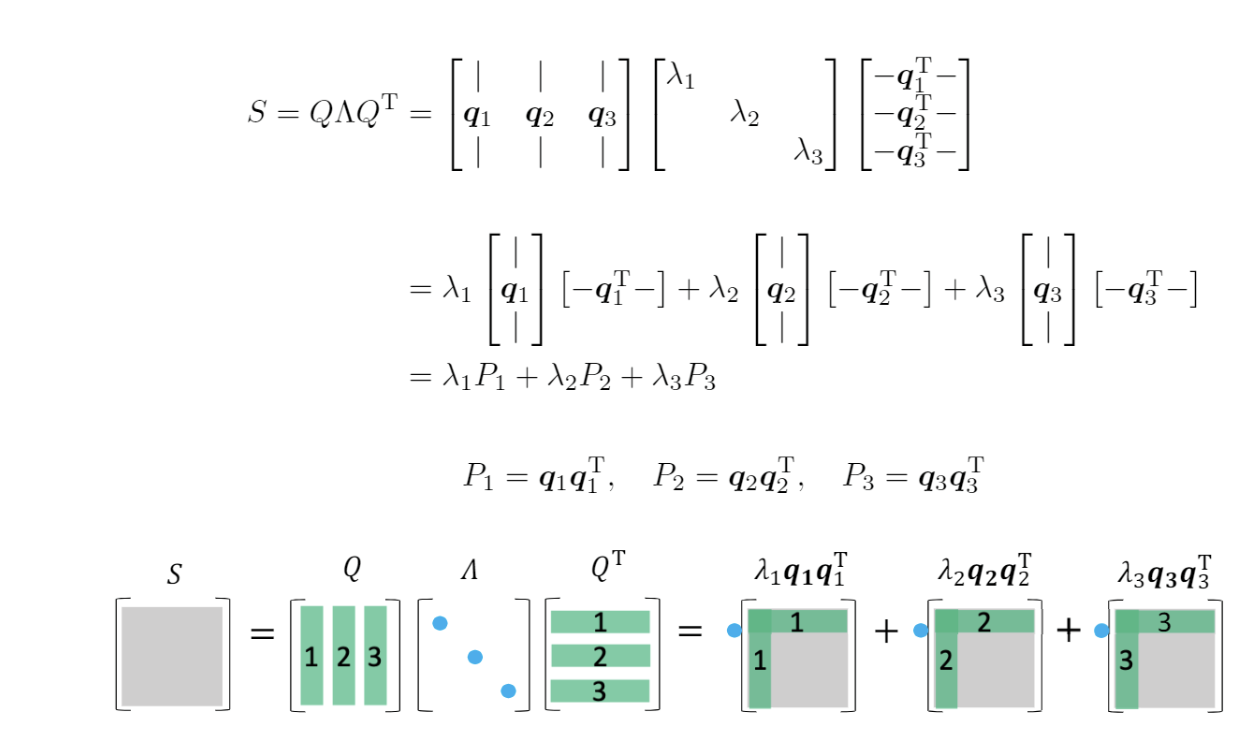
实对称矩阵S必定可对角化,且一定可以选取两两正交的的单位特征向量,使得X为正交矩阵Q,这时原式可以写成这样。
下面,我们将要把实对称矩阵推广到所有正规矩阵,将正交矩阵推广到复数域的酉矩阵。
通向SVD的基础:谱定理
定义:对称矩阵
若A=A∗,称A为对称矩阵(symmetric matrix)。
这里的A∗=AT,表示A的共轭转置(conjugate transpose)。
定义:酉矩阵
若U∗U=UU∗=I,称方阵U为酉矩阵(unitary matrix)
推论U∗=U−1
定义:正规矩阵
若AA∗=A∗A,称方阵A为正规矩阵(normal matrix)。
显然,对称矩阵和酉矩阵都是正规矩阵
谱定理(Spectral Theorem)
谱定理在线性代数里可以这样表述
A是正规矩阵当且仅当存在酉矩阵U,使得
A=UΛU∗(2)
其中Λ为对角阵。
结合特征值分解和酉矩阵的定义,不难发现(2)其实就是一种特殊的特征值分解A=UΛU−1,Λ就是特征值组成的对角阵Λ=diag(λ1,λ2,…,λn)。
证明
必要性
AAA∗A∗A=UΛU∗=UΛU∗UΛU∗=UΛΛU∗=UΛU∗UΛU∗=UΛΛU∗
其中ΛΛ=ΛΛ=diag(∣λ1∣2,∣λ2∣2,…,∣λn∣2)。 故AA∗=A∗A,A为正规矩阵。
充分性
使用数学归纳法,当n=1,结论显然成立。 若谱定理对n−1成立,下面证明其对n成立。
任取特征值λ1,和对应的特征向量x1(存在至少一个,一定能取到!),标准化这个特征向量q=∣x1∣x1,则q∗q=1。
Aqq∗Aq=λ1q=λ1q∗q=λ1
任取一组包含q的基,经过Gram-Schmidt 正交化,和标准化,得到酉矩阵(q,q2,…,qn)=(q,Q)
则
q∗Q=Q∗qQ∗Q=0=I(3)(4)
为了对Q∗AQ应用谱定理,需要证明Q∗AQ为正规矩阵。
(Q∗AQ)(Q∗AQ)∗(Q∗AQ)∗(Q∗AQ)=Q∗AA∗Q=Q∗A∗AQ
由A正规AA∗=A∗A,得Q∗AQ正规。
由谱定理对于n−1成立,应用(2)式,有
Q∗AQ=VΛ1V∗(5)
其中Λ1,V均符合谱定理的描述的性质。
令
U=(qQV)
根据(3),(4)
U∗U=(q∗qV∗Q∗qq∗QVV∗Q∗QV)=I
故U是酉矩阵
U∗AU=(q∗AqV∗Q∗Aqq∗AQVV∗Q∗AQV)
根据(5)有
AQVV∗Q∗AV∗Q∗AQV=QVΛ1=Λ1V∗Q∗=Λ1
则
U∗AU=(λ1q∗qΛ1V∗Q∗qq∗QVΛ1Λ1)=(λ1Λ1)=Λ
故原命题A=UΛU∗得证。
参考
https://github.com/kenjihiranabe/The-Art-of-Linear-Algebra/tree/main
https://inst.eecs.berkeley.edu/~ee127/sp21/livebook/thm_sed.html
Introduction to Linear Algebra, 5th edition, by Gilbert Strang