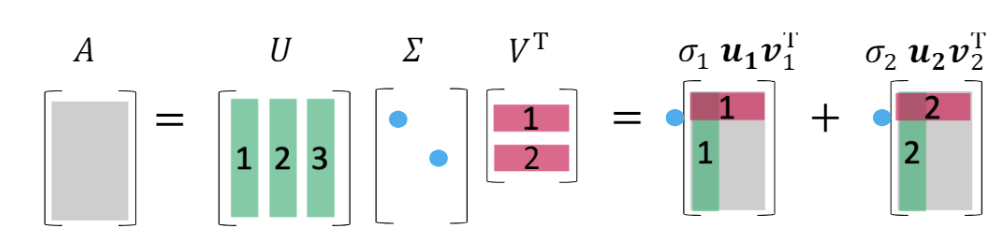理解Cookie、Session和Token
身份验证
Web应用经常需要对用户进行身份验证,才能判定用户的权限,决定用户能访问哪些资源。比如只有你才能看到自己的私密QQ相册,比如只有老师才能看到智学网中全班同学的成绩,同学只能看到自己的。
身份验证需要在服务器和客户端之间交换和保存数据,比如当你登录了一个网站,你并不希望下次登录的时候还要输入账号密码,需要建立一些机制,保存这个登录的状态,告诉服务器“是我,我不久前刚刚登录过”。于是就有了以下这些概念。
Cookie
cookie,就是曲奇饼干一小段储存在客户端(浏览器)的数据。cookie可以用来保存状态,不仅仅是账户的登录状态,也可能包括一些设置、浏览记录等。
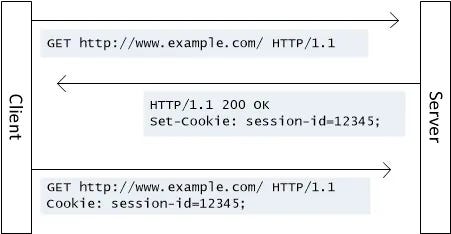
cookie是由服务器生成,储存在客户端的数据。目的是为了保存一些状态,让服务器知道这次请求和之前的请求发送自相同的客户端。
机制
当服务器想要向客户端添加cookie的时候,服务器会在response headers中添加Set-Cookie项,然后浏览器会保存Set-Cookie中的值。之后每次访问相同站点的时候,都会带上相同的数据,放在Cookie中。当然,服务器那里也要保存一份cookie,用于比对验证。
用 ...
基于SVD的图像压缩算法
理论基础
详见奇异值分解
奇异值分解(SVD)可以将任意矩阵分解为A=u1σ1v1∗+u2σ2v2∗+⋯+urσrvr∗=UΣVT\boldsymbol{A}=\boldsymbol{u}_1\sigma_1\boldsymbol{v}^* _1 + \boldsymbol{u}_2\sigma_2\boldsymbol{v}^* _2 + \dots + \boldsymbol{u}_r\sigma_r\boldsymbol{v}^*_r=\boldsymbol{U \Sigma V}^\mathrm{T}A=u1σ1v1∗+u2σ2v2∗+⋯+urσrvr∗=UΣVT的形式。并且越靠近后面的项越不重要,去除它们就可以用更小的空间储存一个与原来矩阵相近的矩阵。
若将图像看作RGB三通道的三个矩阵,对图像SVD并保留前kkk项,就可以实现图像压缩。
效果展示&分析
可以看到,当压缩率在0.5以上时,图像基本保持原本的细节,压缩率0.5以下时,逐渐丢失了细节。
画出σk\sigma_kσk曲线。可以看到σk\sigma_kσk随kkk的增加先急剧降低,后 ...
奇异值分解(SVD)
前置知识
见另一篇博客:谱定理的证明
奇异值分解(SVD)
奇异值分解(singular value decomposition, SVD),说的是任意矩阵A∈Cm×n\boldsymbol{A} \in \mathbb{C}^{m\times n}A∈Cm×n,都可以分解成以下形式
A=u1σ1v1∗+u2σ2v2∗+⋯+urσrvr∗=(u1…u2um)(diag(σ1,σ2,…,σr)000)(v1∗v2∗⋮vn∗)=UΣV∗\begin{align*}
\boldsymbol{A}&=\boldsymbol{u}_1\sigma_1\boldsymbol{v}^* _1 + \boldsymbol{u}_2\sigma_2\boldsymbol{v}^* _2 + \dots + \boldsymbol{u}_r\sigma_r\boldsymbol{v}^*_r \\
&= \left(\begin{array}{c}
\boldsymbol{u}_1 & \dots & \boldsymbol{u}_2 & \boldsymbol{ ...
谱定理(Spectral Theorem)的证明
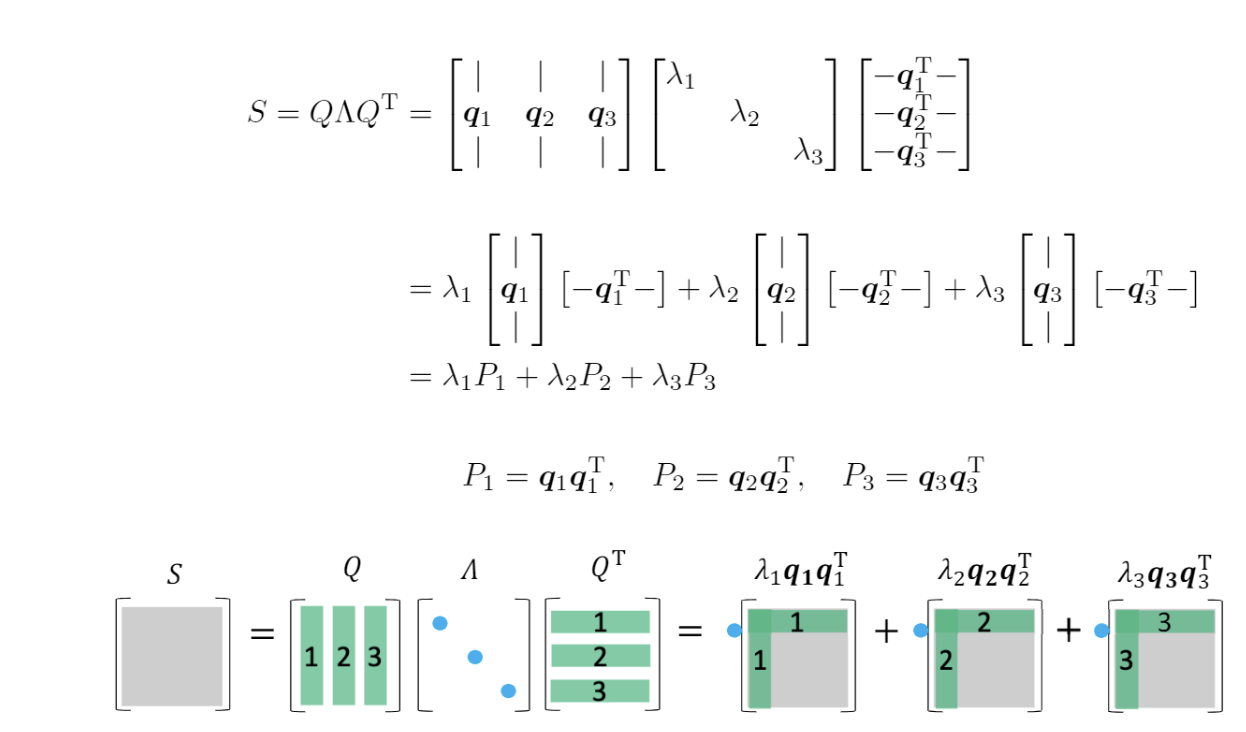
回顾特征值分解/对角化
定义
对于n×nn \times nn×n的方阵A\boldsymbol{A}A,如果有下面的等式:
Ax=λx\boldsymbol{Ax}=\lambda \boldsymbol{x}
Ax=λx
其中x\boldsymbol{x}x为非零向量。
我们就称x\boldsymbol{x}x是x\boldsymbol{x}x的一个特征向量(eigenvector),λ\lambdaλ是x\boldsymbol{x}x的一个特征值(eigenvalue)。
求解
Ax=λIx(A−λI)x=0det(A−λI)=0\begin{align*}
\boldsymbol{Ax} &= \lambda \boldsymbol{Ix} \\
(\boldsymbol{A} - \lambda \boldsymbol{I})\boldsymbol{x} &= \boldsymbol{0} \\
\det(\boldsymbol{A} - \lambda \boldsymbol{I}) &= 0 \\
\end{align*}Ax(A−λI)xdet ...
线性代数中的投影
投影矩阵的推导
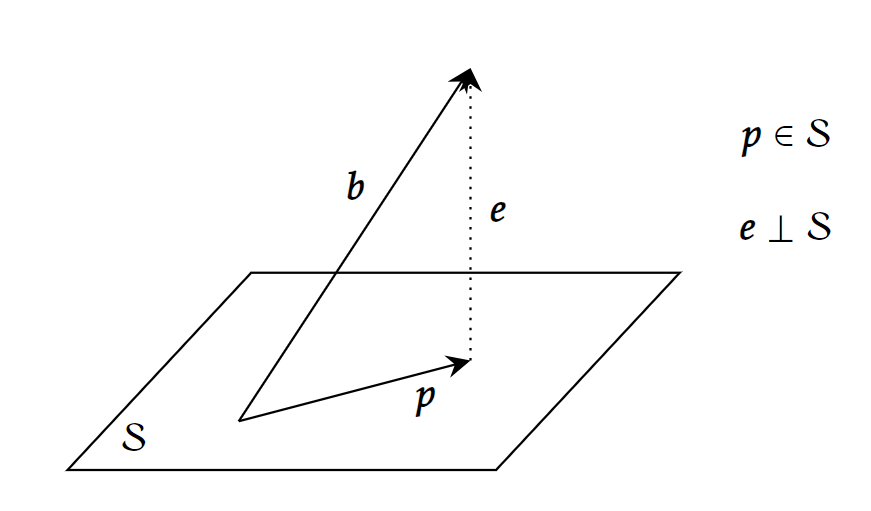
假设我们想把一个向量b\boldsymbol{b}b投影到线性空间S\mathcal{S}S中,应该怎么做呢。
设投影后的向量为p\boldsymbol{p}p,则有p∈S\boldsymbol{p}\in \mathcal{S}p∈S,设误差向量(error vector)e=b−p\boldsymbol{e}=\boldsymbol{b}-\boldsymbol{p}e=b−p,则e\boldsymbol{e}e应与S\mathcal{S}S正交。投影就是将向量分为两部分b=p+e\boldsymbol{b}=\boldsymbol{p}+\boldsymbol{e}b=p+e,一部分在S\mathcal{S}S中,另一部分与S\mathcal{S}S正交,然后取其中的p\boldsymbol{p}p。也可以用图像直观理解:
要求得p\boldsymbol{p}p,只需要将p∈S (1)\boldsymbol{p}\in \mathcal{S}\;\mathrm{(1)}p∈S(1)和e⊥S (2)\boldsymbol{e}\perp \mathcal{S ...
NumPy学习笔记
NumPy是一个广泛使用的Python库,NumPy是Numerical Python的缩写,用于多维数组的计算,并且支持对多维数组进行各种数学处理,同时保持非常高的性能。Pandas, SciPy, Matplotlib, scikit-learn等一系列库都使用了NumPy提供的多维数组。
安装
使用Anaconda(推荐)
推荐使用Anaconda安装NumPy
1conda install numpy
使用pip
1pip install numpy
引入NumPy
1import numpy as np
将NumPy重命名为np不仅能让代码简短,还是一种约定俗成的写法,建议任何时候都这么写。
NumPy中的数组和Python原生的list有什么区别?
不同点
NumPy array
Python list
元素类型
数组的所有元素必须拥有相同类型
数组的元素可以有不同的类型
内存占有
内存占用少
有额外的内存占用
性能表现
速度快
速度较慢
数组
数组是NumPy的核心。在NumPy中,数组被称作ndarray,是多维数组(N-Dimension ...
一看就懂的Linux Shell的基础使用(二)
脚本
bash不仅可以直接输入到命令行执行,也可以作为一种脚本语言。作为一种脚本语言,Bash也拥有变量、分支语句、循环语句等。
可以在某个文件里写bash脚本,然后运行它,不必每次都在命令行里输入。将以下代码保存到hello.sh里,.sh后缀代表这是一个bash脚本,当然,使用其他后缀也不影响脚本正常运行。
12#!/bin/bashecho "Hello World!"
文件的第一行是#!/bin/bash,以#开始的内容是注释,意味着不会被运行。但是在文件的最开始,以#!开头的注释有个特别的名字,它被称作“shebang”,可以提示系统,使用什么程序来解析下面的代码。这里的#!/bin/bash,告诉操作系统使用/bin/bash解释下面的代码,也可以写作#!/bin/sh,因为/bin/sh是一个指向bin/bash的软链接。
在执行之前,请先向这个文件添加执行的权限,因为Linux默认的新文件权限是644,即rw-r--r--,任何人都无法执行。使用chmod +x hello.sh来添加执行权限。
然后,有两种方式可以运行脚本,第一种是输入./hel ...
非对称加密算法与RSA
非对称加密
以下内容引自维基百科:非对称加密
公开密钥密码学(英语:Public-key cryptography)也称非对称式密码学(英语:Asymmetric cryptography)是密码学的一种算法,它需要两个密钥,一个是公开密钥,另一个是私有密钥;公钥用作加密,私钥则用作解密。使用公钥把明文加密后所得的密文,只能用相对应的私钥才能解密并得到原本的明文,最初用来加密的公钥不能用作解密。由于加密和解密需要两个不同的密钥,故被称为非对称加密;不同于加密和解密都使用同一个密钥的对称加密。公钥可以公开,可任意向外发布;私钥不可以公开,必须由用户自行严格秘密保管,绝不透过任何途径向任何人提供,也不会透露给被信任的要通信的另一方。
基于公开密钥加密的特性,它还能提供数字签名的功能,使电子文件可以得到如同在纸本文件上亲笔签署的效果。
对称密码是指在加密和解密时使用同一个密钥的方式,公钥密码则是指在加密和解密时使用不同密钥的方式。
对称密钥加密牵涉到密钥管理的问题,尤其是密钥交换,它需要通信双方在通信之前先透过另一个安全的渠道交换共享的密钥,才可以安全地把密文透过不安全的渠道发送;对 ...
用Python写爬虫的实例一则
将学到的爬虫知识运用到实践中去吧!
要爬的网站是https://quanben-xiaoshuo.com/,这是一个小说网站,目标是可以下载给定小说的所有章节,并保存到本地文件。
开始
首先,我选择的 Python 库是 requests 和 lxml,如果你没有安装这两个库,可以使用 pip install requests 和 pip install lxml 来安装
requests 用来发送请求并获得网页,lxml 用来解析网页,并使用 XPath 找到要获取的数据的位置,如果你不熟悉 XPath,可以看看我的这一篇文章 XPath语法参考
假如你更喜欢css选择器的风格,可以使用 beautifulsoup 这个库,两个库都很方便的
使用requests库获取网页内容
打开要爬取的页面https://quanben-xiaoshuo.com/n/wozaishourendaludangjisi/xiaoshuo.html,看到以下内容:
打开 Python 交互式编辑器,输入以下代码:
123456Python 3.11.4 (tags/v3.11.4:d2340ef, ...
一看就懂的Linux Shell的基础使用(一)
前言
最近在学习MIT的“计算机科学教育中缺失的一课(The Missing Semester of Your CS Education)”,这篇博客既是shell常用命令的备忘,也是这门课程的学习笔记。
shell
shell是操作系统为用户提供交互界面的命令行解释器的统称,例如Windows中的cmd就是一种shell。Bash 是其中最流行的一种。Bash 是 Bourne Again shell 的简称,其他的shell还有:zsh、fish、csh等。
你需要使用一个类Unix shell来完成文中所提到的操作。你可以:
使用安装了Linux的电脑
使用Linux虚拟机
使用WSL(Windows Subsystem for Linux)。
使用shell
进入shell,可以看到这样的一行提示:
1cyrus:~$
cyrus代表当前用户的用户名,也可以使用echo $USER来查看;
~代表当前所在路径,也可以使用pwd来查看;
$是命令提示符,提示用户现在可以输入命令了。
~是表示用户的家目录,非root用户的~代表/home/$USER/,而root用户的~ ...