非对称加密

以下内容引自维基百科：非对称加密

公开密钥密码学（英语：Public-key cryptography）也称非对称式密码学（英语：Asymmetric cryptography）是密码学的一种算法，它需要两个密钥，一个是公开密钥，另一个是私有密钥；公钥用作加密，私钥则用作解密。使用公钥把明文加密后所得的密文，只能用相对应的私钥才能解密并得到原本的明文，最初用来加密的公钥不能用作解密。由于加密和解密需要两个不同的密钥，故被称为非对称加密；不同于加密和解密都使用同一个密钥的对称加密。公钥可以公开，可任意向外发布；私钥不可以公开，必须由用户自行严格秘密保管，绝不透过任何途径向任何人提供，也不会透露给被信任的要通信的另一方。

基于公开密钥加密的特性，它还能提供数字签名的功能，使电子文件可以得到如同在纸本文件上亲笔签署的效果。

对称密码是指在加密和解密时使用同一个密钥的方式，公钥密码则是指在加密和解密时使用不同密钥的方式。

对称密钥加密牵涉到密钥管理的问题，尤其是密钥交换，它需要通信双方在通信之前先透过另一个安全的渠道交换共享的密钥，才可以安全地把密文透过不安全的渠道发送；对称密钥一旦被窃，其所作的加密将即时失效；而在互联网，如果通信双方分隔异地而素未谋面，则对称加密事先所需要的“安全渠道”变得不可行；非对称加密则容许加密公钥随便散布，解密的私钥不发往任何用户，只在单方保管；如此，即使公钥在网上被截获，如果没有与其匹配的私钥，也无法解密，极为适合在互联网上使用。

另一方面，公钥解密的特性可以形成数字签名，使数据和文件受到保护并可信赖；如果公钥透过数字证书认证机构签授成为电子证书，更可作为数字身份的认证，这都是对称密钥加密无法实现的。

不过，公钥加密在在计算上相当复杂，性能欠佳、远远不比对称加密；因此，在一般实际情况下，往往通过公钥加密来随机建立临时的对称秘钥，亦即对话键，然后才通过对称加密来传输大量、主体的数据。

对称加密很符合直觉，就和我们日常生活中的一把钥匙开一把锁，需要使用同一把钥匙加锁和开锁。但是这有一个问题：

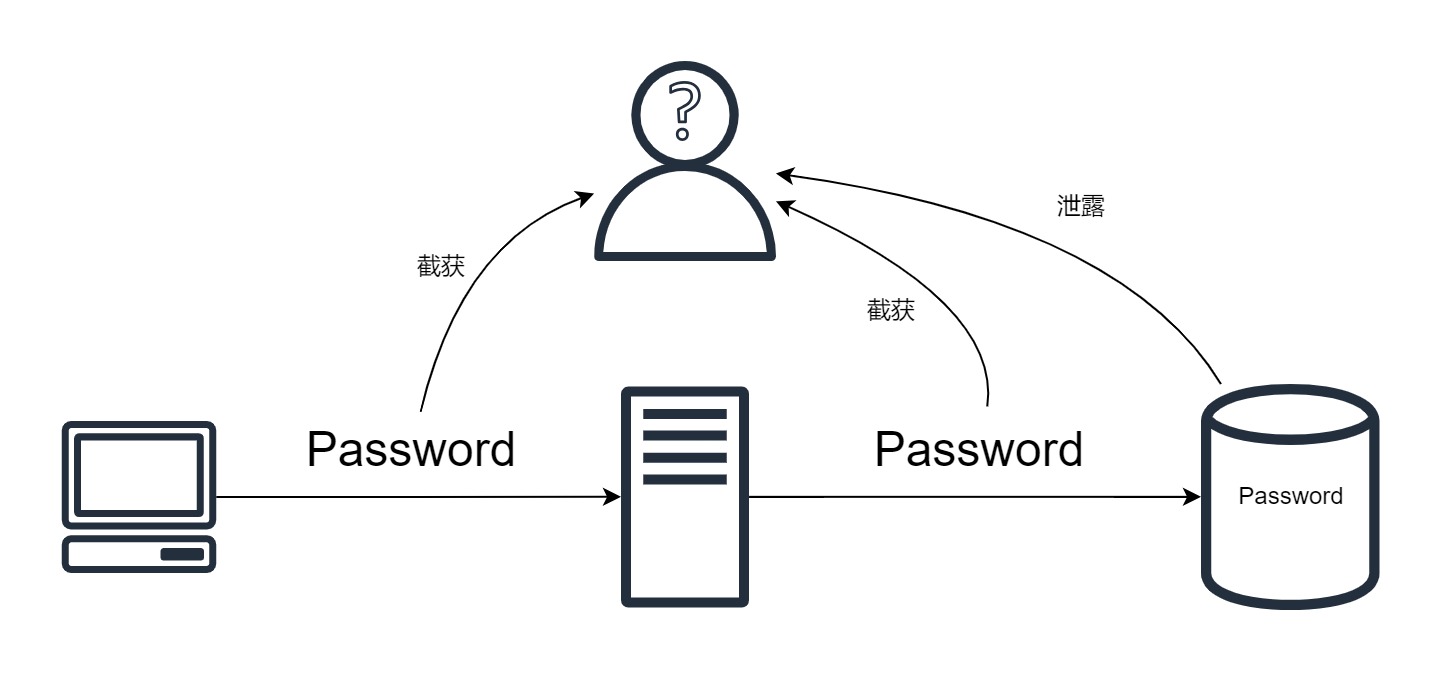
假设有两个人分别叫做Alice和Bob，他们想要交换信息，但是不想要让第三人Eve知道他们在交流什么。Alice使用对称加密生成了一把钥匙，然后将信件用钥匙锁在箱子里，再把箱子寄给Bob。

问题是，Bob需也要钥匙来打开箱子，Alice如果把钥匙也寄给Bob，没准Eve就会截获这个快递，拿到钥匙，进而知道一切。

而非对称加密是一种神奇的加密方式，它会给你两把钥匙，用一把锁上箱子，就必须使用另一把打开。

Alice使用非对称加密生成了一对密钥，将其中一把钥匙公开，称作 公钥 ，另一把Alice自己好好保管，不让别人得到，称作 私钥 。那么这两把钥匙就可以完成这些神奇的操作：

  • 验证身份：
    Alice在发布消息的时候使用私钥加密，将密文发送给Bob，如果Bob可以使用公钥成功解密密文，说明这个消息就是Alice发来的。其他人无法冒充Alice发消息，因为他们没有Alice的私钥。这里非对称加密起到了 数字签名 的效果。
  • 加密通信：
    现在Bob要给Alice发消息，但是Bob不想要让别人知道他给Alice发了什么，Bob可以将明文用公钥加密，这样只有掌握了私钥的Alice可以看到明文。

非对称加密一般需要耗费更长的时间，使用非对称加密交换大量的信息会拖慢传递信息的速度。因此在实践中，会先使用非对称加密传递对称加密的密钥，再使用对称加密传递信息。

RSA算法

而RSA是非对称加密的一种实现方法，它的可靠性建立于大数的质因数分解的计算难度，要理解RSA算法的实现，你需要先了解一些数论的前置知识。

以下内容引自维基百科：RSA加密算法

RSA加密算法是一种 非对称加密算法 ，在公开密钥加密和电子商业中被广泛使用。

对极大整数做因数分解的难度决定了 RSA 算法的可靠性。换言之，对一极大整数做因数分解愈困难，RSA 算法愈可靠。假如有人找到一种快速因数分解的算法的话，那么用 RSA 加密的信息的可靠性就会极度下降。但找到这样的算法的可能性是非常小的。今天只有短的 RSA 钥匙才可能被强力方式破解。到2020年为止，世界上还没有任何可靠的攻击RSA算法的方式。只要其钥匙的长度足够长，用RSA加密的信息实际上是不能被破解的。

数学推导

前置知识：费马小定理和欧拉定理

先找到两个大质数 p,qp,q （这两个数越大加密越安全，但相应地，计算也会变慢）

计算它们的积 n=pqn=pq

计算 nn 的欧拉函数 φ(n)=(p−1)(q−1)\varphi(n)=(p-1)(q-1)

找到一个 ee 满足 e≤ne \leq n 且 gcd⁡(e,n)=1\gcd(e,n)=1 （ee 的选取要让 me>nm^e > n，否则直接对密文 cc 开 ee 次根就会得到明文）

计算 ee 模 φ(n)\varphi(n) 的逆元 dd，即

ed≡1(modφ(n))ed \equiv 1 \pmod{\varphi(n)}

则两个二元组 (e,n),  (d,n)(e,n),\;(d,n) 就为一对密钥。

加密和解密的过程是一样的，只需要将文本转化为一个正整数，然后进行模 nn 意义下的指数运算。

取假设需要加密的明文为 mm ，mm 需要满足 m<nm < n，这样才能保证模 nn 之后 mm 不变。

则用 (e,n)(e,n) 加密 mm 后的密文为

c≡me(modn)c\equiv m^e\pmod{n}

再使用 (d,n)(d,n) 解密

cd≡med≡med mod φ(n)≡m(modn)c^d\equiv m^{ed}\equiv m^{ed\bmod\varphi(n)}\equiv m\pmod{n}

就得到了明文。

代码实现

代码实现只作为示范，实际运用请使用一些密码学的库，它们经过验证、功能更丰富、效率更高，比如 Python 的 pycrypto、JS 的 cryptico 库等。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
# 仅供理解RSA使用，请不要用在真正的加密场景
import math, random

def millerRabin(n, test_time):
    '''
    使用 miller rabin 素性测试检验是否是一个素数
    test_set 是用来进行测试的 a 的集合
    miller rabin 是一个概率算法，有概率将合数误判为素数，
    但是只要测试次数足够多，出错的可能性非常低，
    因此这里可以使用 miller rabin 素性测试
    '''
    if n % 2 == 0:
        return n == 2
    r, s = 0, n - 1
    while s % 2 == 0:
        r += 1
        s //= 2
    for i in range(test_time):
        a = random.randint(2, n-1)
        x = pow(a, s, n)
        if x == 1 or x == n - 1:
            continue
        for _ in range(r - 1):
            x = x * x % n
            if x == n - 1:
                break
        else:
            return False
    return True

def isPrime(n):
    return millerRabin(n, 100)

def randCond(l, r, cond):
    n = random.randint(l, r)
    while not cond(n):
        n = random.randint(l, r)
    return n

def genPrime(l):
    '''
    返回二进制长度为 l 的随机素数
    '''
    return randCond(1<<l-1, (1<<l)-1, isPrime)

def genRsaKey(l):
    '''
    返回二元组，分别是公钥和私钥
    l: n 的二进制长度
    '''
    p = genPrime(l//2 + 1)
    q = genPrime(l//2 + 1)
    n = p * q 
    phin = (p-1)*(q-1)
    # e 可以取任意小于 phi(n)=(p-1)*(q-1) 且与 phi(n) 互质的数，为了方便可以直接取一个固定的质数如65537，这里使用随机数
    e = randCond(3, phin - 1, lambda x: math.gcd(x, phin) == 1)
    d = pow(e, -1, phin)
    return (e, n), (d, n)

def Rsa(m, key):
    return pow(m, *key)


LENGTH = 512

def Test(test_time):
    for i in range(test_time):
        pub, pri = genRsaKey(LENGTH)
        m = random.randint(2, (1<<LENGTH-1)-1)
        assert Rsa(Rsa(m, pub), pri) == m

if __name__ == '__main__':
    pub_key, pri_key = genRsaKey(LENGTH)
    print(f"e: {hex(pub_key[0])[2:]}")
    print(f"d: {hex(pri_key[0])[2:]}")
    print(f"n: {hex(pub_key[1])[2:]}")

    m = input(f'enter a message (no more than {LENGTH//8} ascii characters): ').encode('ascii')
    l = len(m)
    m = int.from_bytes(m, 'big') # 转成 int

    c = Rsa(m, pub_key)
    print(f"ciphertext: {hex(c)[2:]}")

    m2 = Rsa(c, pri_key)
    m2 = m2.to_bytes(l, 'big').decode('ascii')
    print(f"plaintext: {m2}")


运行程序

1
2
3
4
5
6
e: 408f68187d69b88ea64d0b516864d19a98daa137d8a9fdbc54aa38290252ac9bfc7a4d4b366b2da3b8cff0ab658676d41652c3f899455db438ff22d29a799f21
d: 251672123c6a1bf9aa22fc171ed58905d205404864c1ae0ab9b586911d43c5334e2664d0db813b0225b66088405e523569c083986ff299b3b03777f2822c4e831
n: 2ab2a544ef5a7f5b701b6cb80fb5fffc8a6509f5f2d03ceeefa4190134a393d239914166d31a53a24a124e7cf54b15e3b82644f0c0d4cae9b7f66bf9b41277f6f
enter a message (no more than 64 ascii characters): cyrus28214.top | Think twice, code once.
ciphertext: 16f3fd561d9cc07dd7420f993de007a171a6661f4475d7f0ad4264279c393741e1c0f19089ed60536bc4796c4917ed8887ec60ff4847b61c5a9b4ce7e7829c830
plaintext: cyrus28214.top | Think twice, code once.