CS231n/EECS598 学习笔记（二）Lecture 5-7

Lecture 5

Neural Network

线性分类器的局限

Linear Classifier能做的其实很有限，从Lecture 3的“几何视角”中，我们知道了线性分类相当于画了一个超平面来将超空间分类。然而并非所有情况下样本点都可以被一个平面简单的分割。

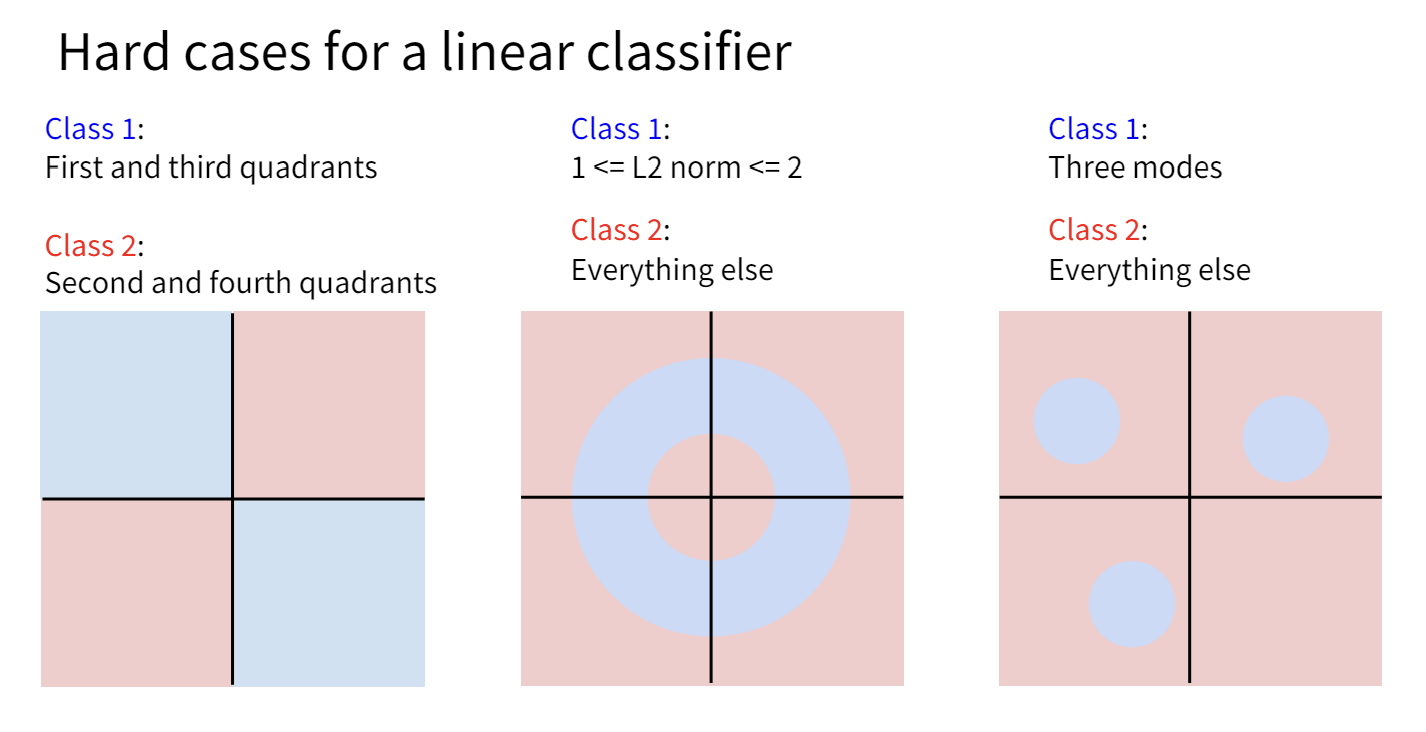
一种方法是对原有数据集做一些变换，使得线性分类器能够分割变换后的数据。

这种方法的确能取得不错的结果，只需要人工提取出数据集的一些特征，然后用这些特征来训练线性分类器。比如，对于图像分类，可以设计算法来提取图像的边缘、颜色、纹理等特征，然后用这些特征来训练线性分类器。同时，也有一些data-driven的方法可以用来提取特征。

但是这种方法的缺点也很明显，就是研究者必须知道哪一些特征变换对于分类是有效的。而神经网络解决了这个问题。

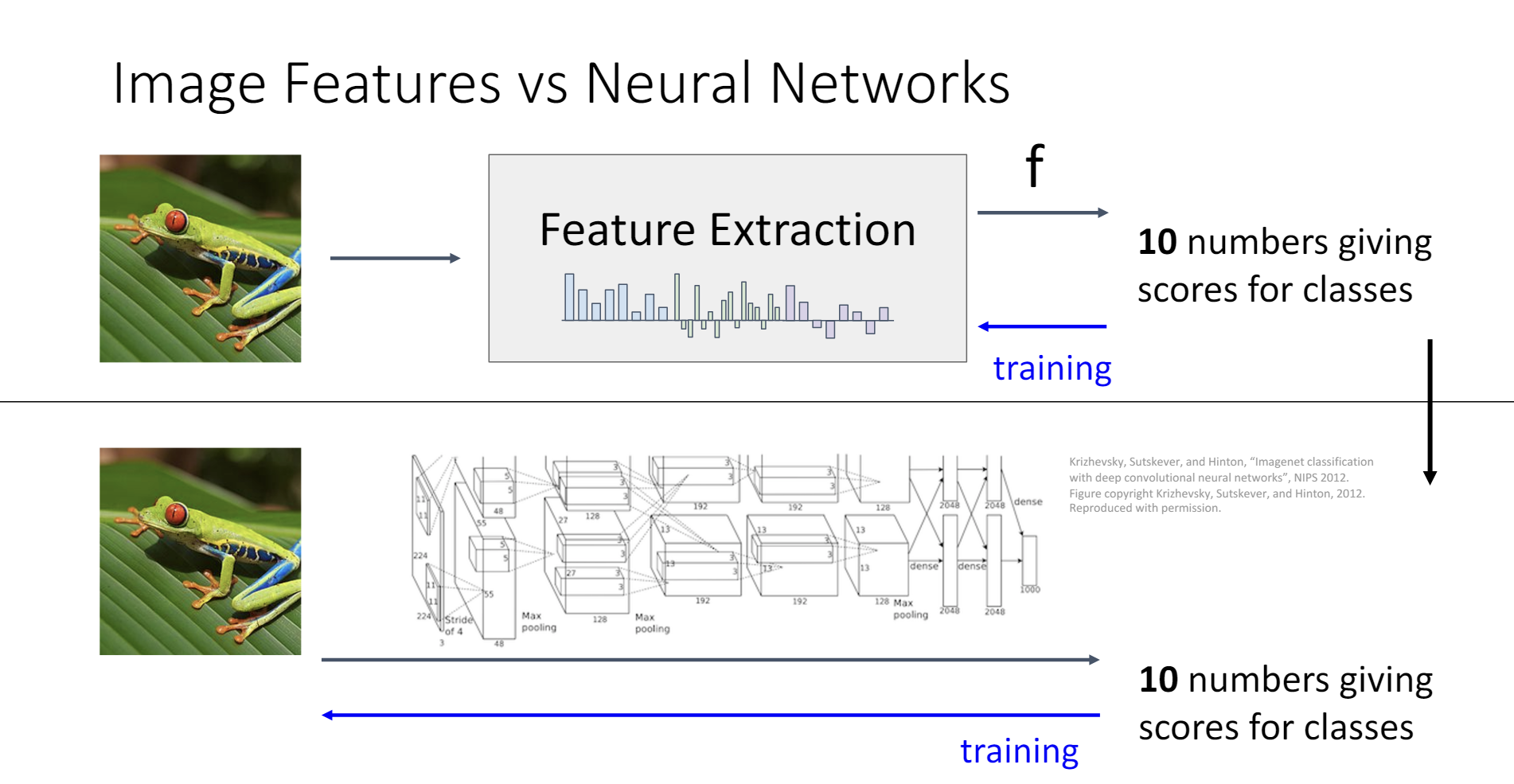
或许，神经网络只是将特征提取的步骤和训练的步骤融合在了一起。

从线性分类器到神经网络

神经网络其实只是线性分类器的叠加

Linear Score Function: $f=\boldsymbol{W}x$
2-layer Neural Network: $f=\boldsymbol{W_2}\sigma(\boldsymbol{W_1}x)$ （省略了bias项）

公式里的 $\sigma$ 马上就会提到。

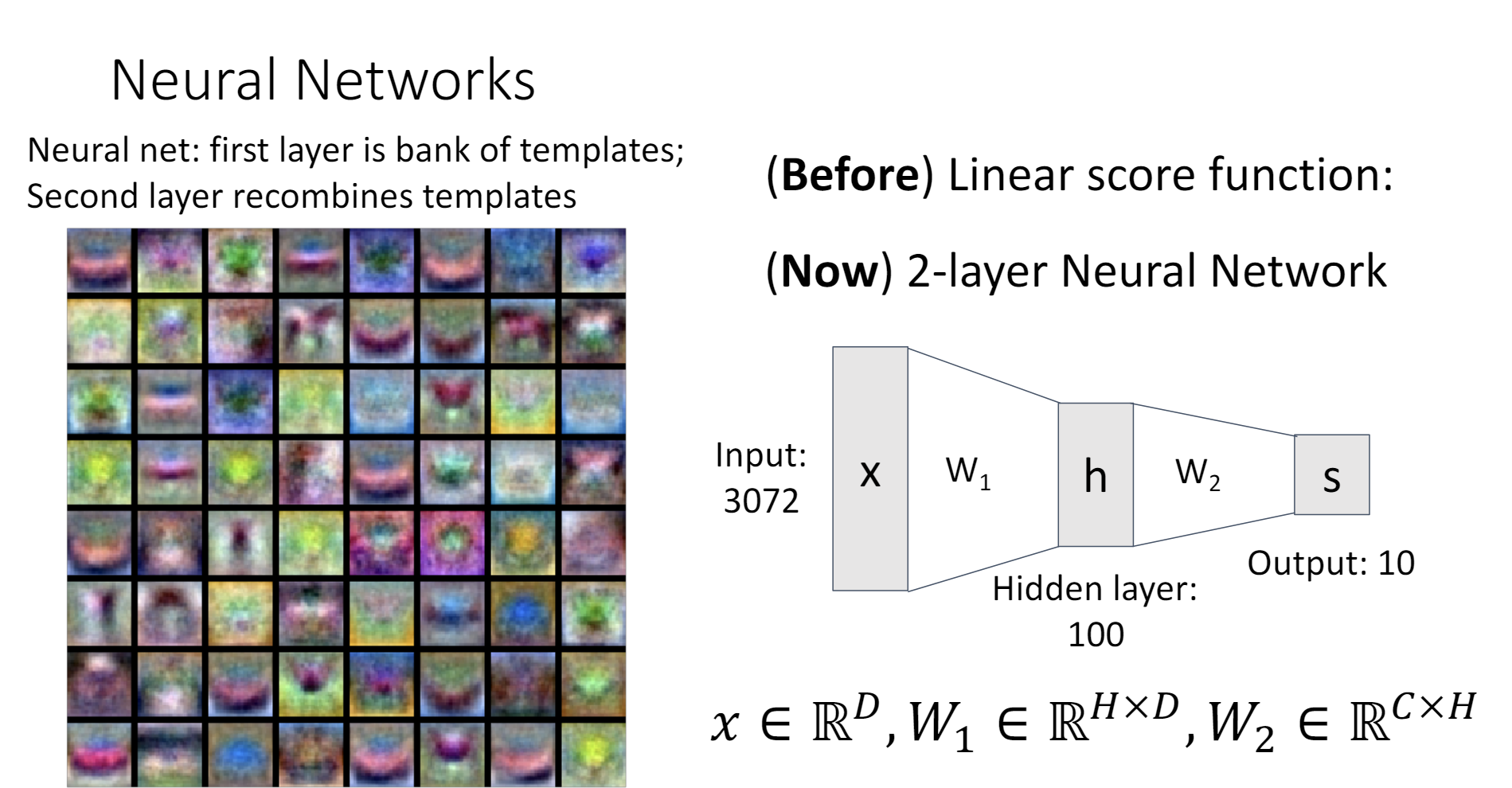
在Lecture 3中，有一种理解线性分类器的视角是把权重矩阵看作是若干个“模版”，而输出代表了图片和每个模版的相似度。

对于两层的神经网络，我们可以这样理解，把第一个权重矩阵看作是一个“模版仓库”，第二个权重矩阵可以自由组合这些模版，从而得到输出。如此一来，隐含层就代表了图片与每一个模版的相似程度，输出就代表了图片与某种模版的组合的相似程度。

之前线性分类器中的模版很容易看出到底是什么物体。但是图片左侧这些神经网络第一层的模版，有一些就不好辨认了。按照我的理解，在第一层的网络中，神经网络更倾向于学习更加基本的特征，这样才能在后续的层里面充分利用，组合这些特征，完成更加高级的任务。

激活函数

在刚刚的神经网络公式里，有一个 $\sigma$ 函数，这个实际上就是神经网络的激活函数。

激活函数对神经网络是必须的，假如一个神经网络 $f=\boldsymbol{W_2 W_1}x$ 没有激活函数，会怎么样？没错，他其实就退化成了一个线性分类器 $f=(\boldsymbol{W_2 W_1})x$ 。我们白费力气地将两个线性分类器堆叠，然后得到了一个新的线性分类器。

激活函数给一大堆线性的矩阵中间加上了非线性的成分，让神经网络得以拟合非线性的函数。

常用的激活函数有这一些：

ReLU是深度学习中最常用的激活函数。

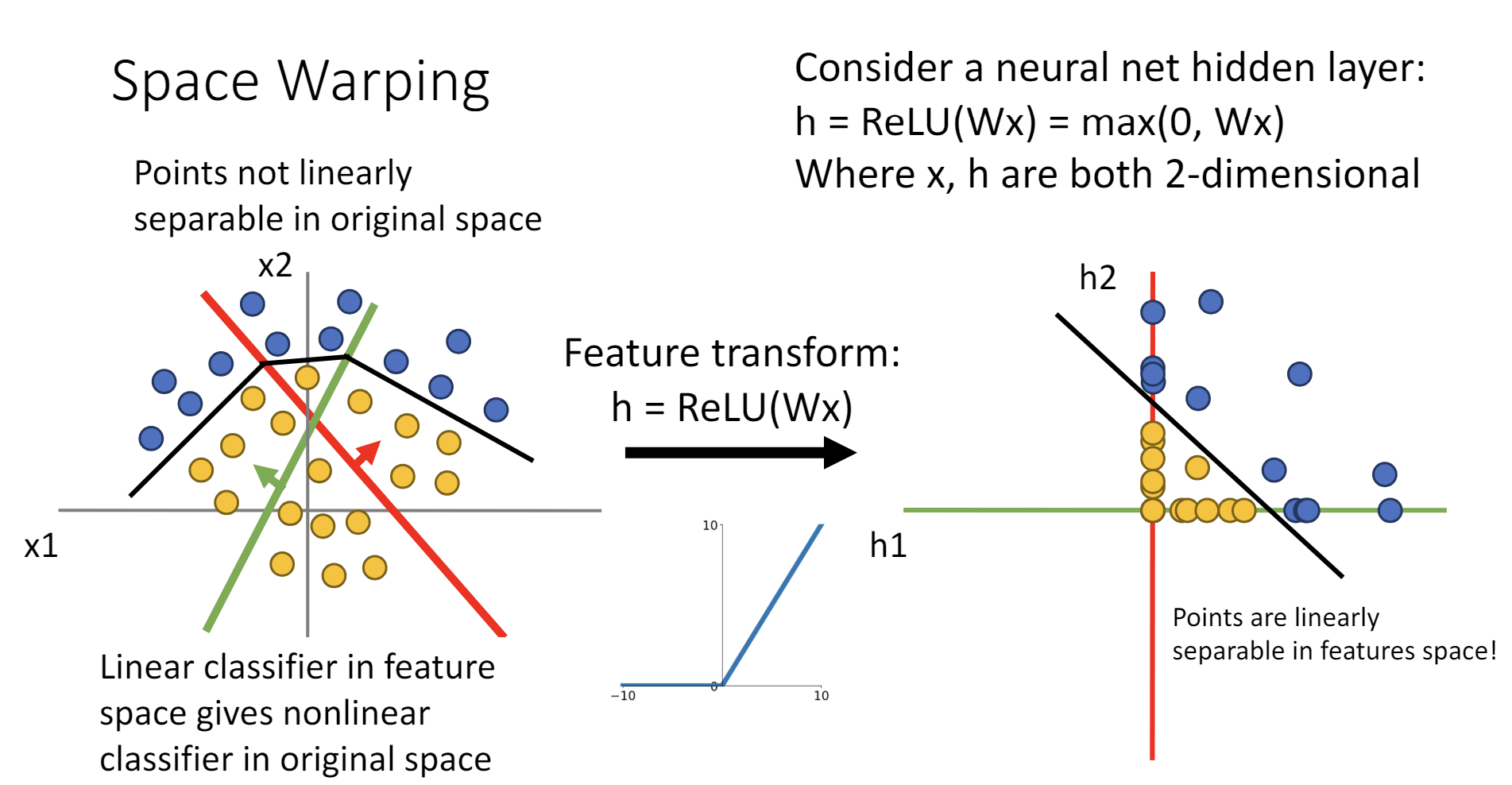
激活函数可以非线性地变换空间，使得线性不可分的点云转化成线性可分的点云。

万能近似定理（Universal Approximation Theorem）

万能近似定理（Universal Approximation Theorem）
单隐含层的神经网络可以拟合任意连续函数 $f: \mathbb{R}^n \rightarrow \mathbb{R}^m$ 。

其证明过程考虑了ReLU作为激活函数的情况，首先构造了一个“bump function”，这个函数在某个位置凸起，其他位置为0，通过线性地组合这个函数，可以拟合任何连续函数。

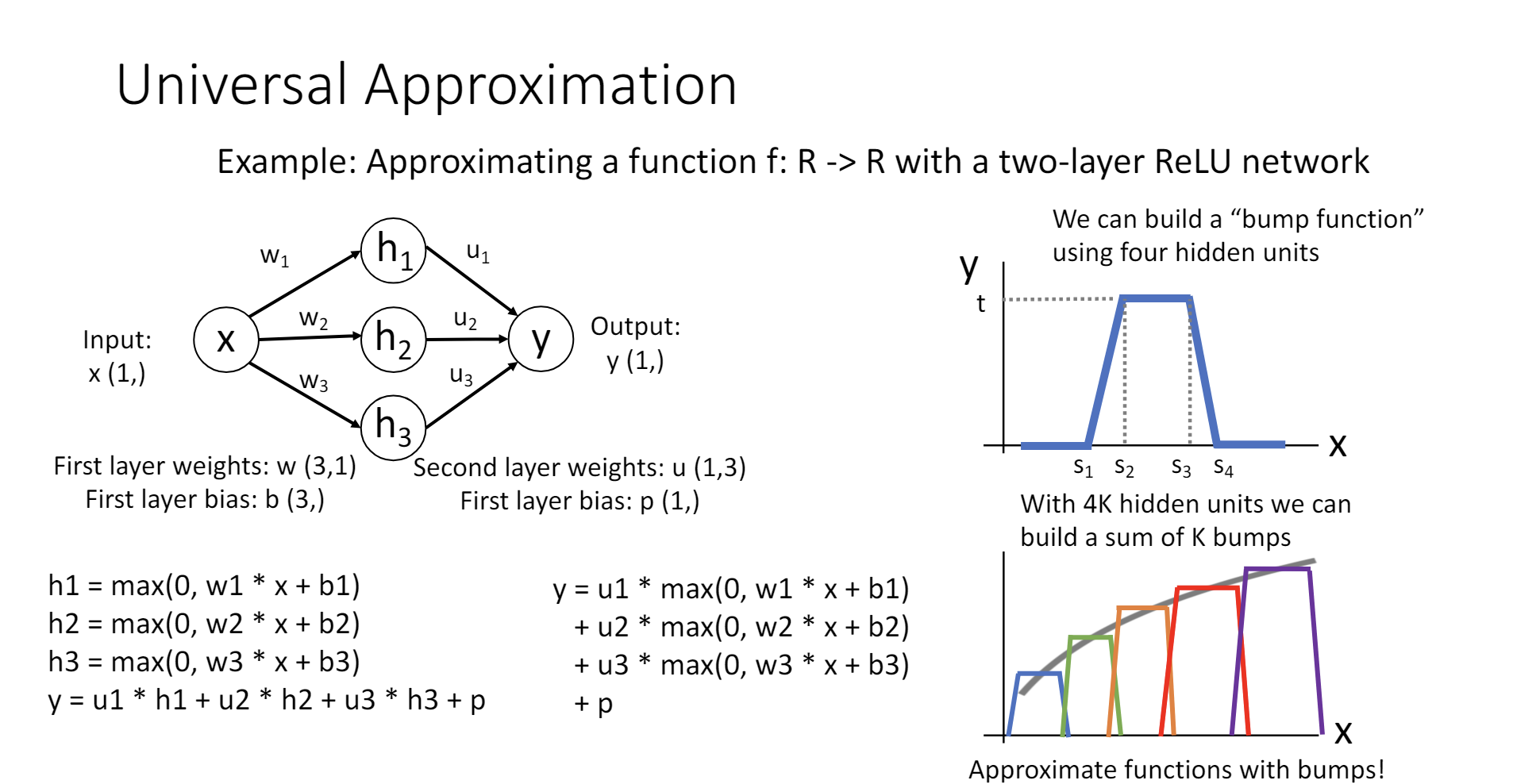
这样的证明有很多细节不严谨，http://neuralnetworksanddeeplearning.com/chap4.html中有更多的讨论。

Universal Approximation的确很cool，但其实只是一种数学上的构造，这个定理解决不了什么工程上的问题，如“我们是否能用SGD拟合这个函数”、“我们需要多少数据才能拟合这个函数？”等。它只是告诉我们有这样一组权值可以让神经网络拟合你想要拟合的函数，但是并没有告诉我们如何找到它。

并且，拟合任意函数看起来是一个很强大的性质，其实不然，简单如K-Means的算法都能做到万能近似。

凸优化

万能近似定理不能保证我们能否找到一组权值来最佳拟合，但是假如我们的目标函数是凸（convex）的，那么相关的理论可以保证，我们就能保证无论选取什么样的初始值，都能找到全局最优解。

线性分类器的优化问题就是一个凸优化问题。对于线性分类器，无论你使用SVM loss还是Softmax，L1正则化还是L2正则化，最终的目标函数都是凸的！这意味着线性分类器可以保证一定收敛到全局最优解，线性分类器的优化问题具有确定性。

然而，很遗憾的是，多层的神经网络并不具有这种性质，神经网络收敛到哪里依赖于随机初始化的值，或是优化的方法，神经网络不一定能收敛到全局最优解，可能陷入局部最优解，甚至不收敛。尽管在工程实践中神经网络取得了许多成功，神经网络的有效性并没有理论的保证，这仍然是一个相当活跃的研究领域。

Lecture 6

误差反向传播

为了优化误差函数，寻找到最优的权值 $W$ ，我们需要计算梯度 $\nabla_W L$ 。

相比手动计算误差函数的梯度，更好的方法是发明一些数据结构和算法来自动计算梯度。

这里的数据结构就是计算图，计算图用图的方式建模了数据在的计算过程。而算法就是反向传播（Back Propagation），我们可以反向遍历计算图来更新整个模型的梯度。这种方法允许我们使用更复杂、更灵活的模型，而无需推导梯度的表达式。

计算梯度时，我们首先正向计算输出，然后反向传播梯度。

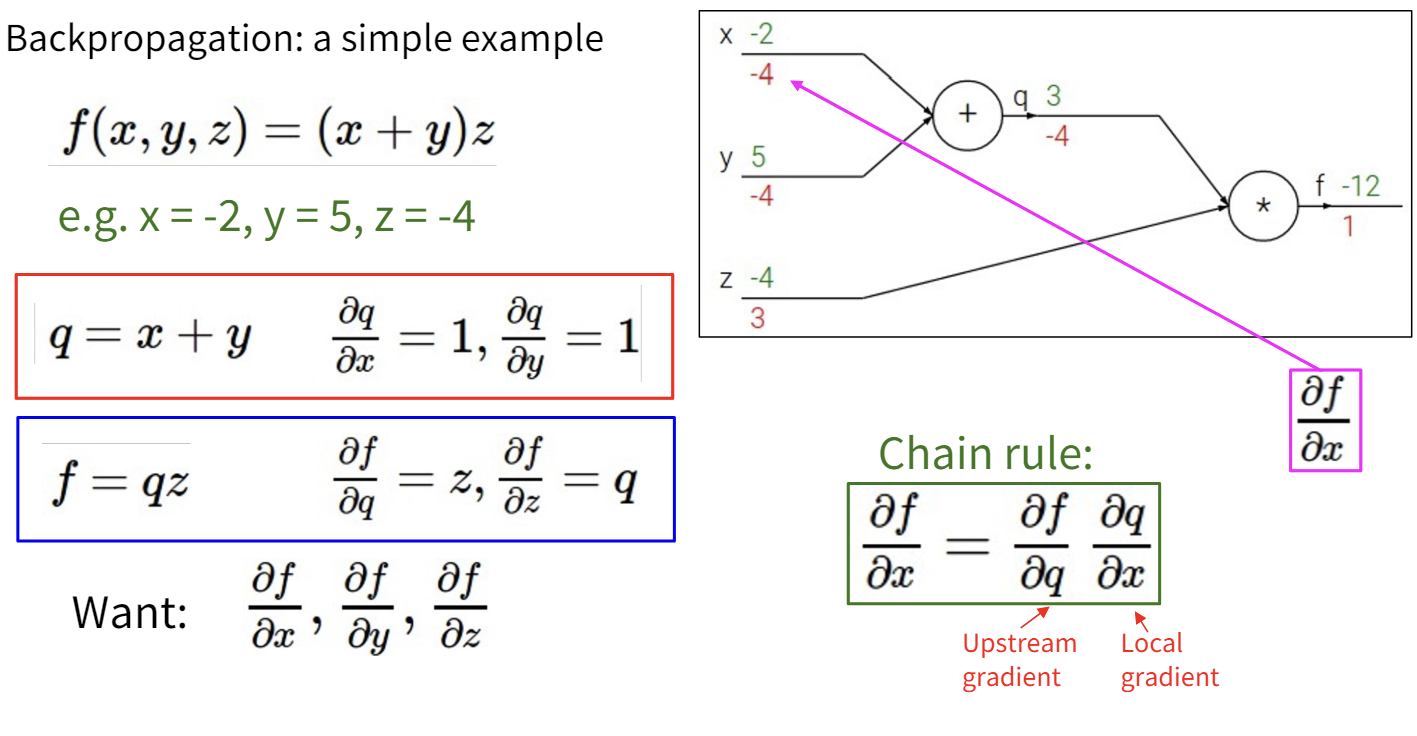
使用计算图和误差反向传播的另一个好处是模块化，我们可以在计算图中定义自己的节点，而不必永远使用最简单的算术原语。

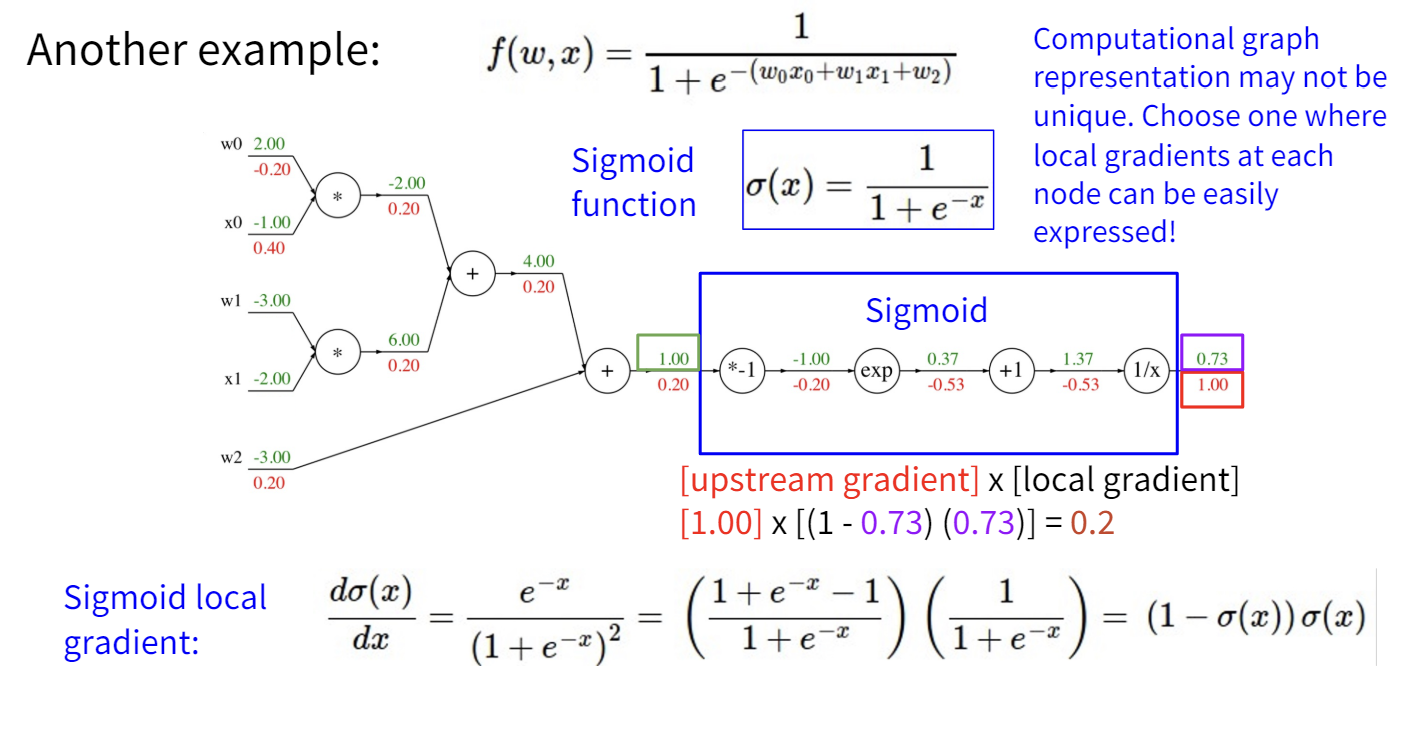
课程提到了一个让我感觉挺新奇的视角，它介绍了这几种门在梯度传播流中的意义。

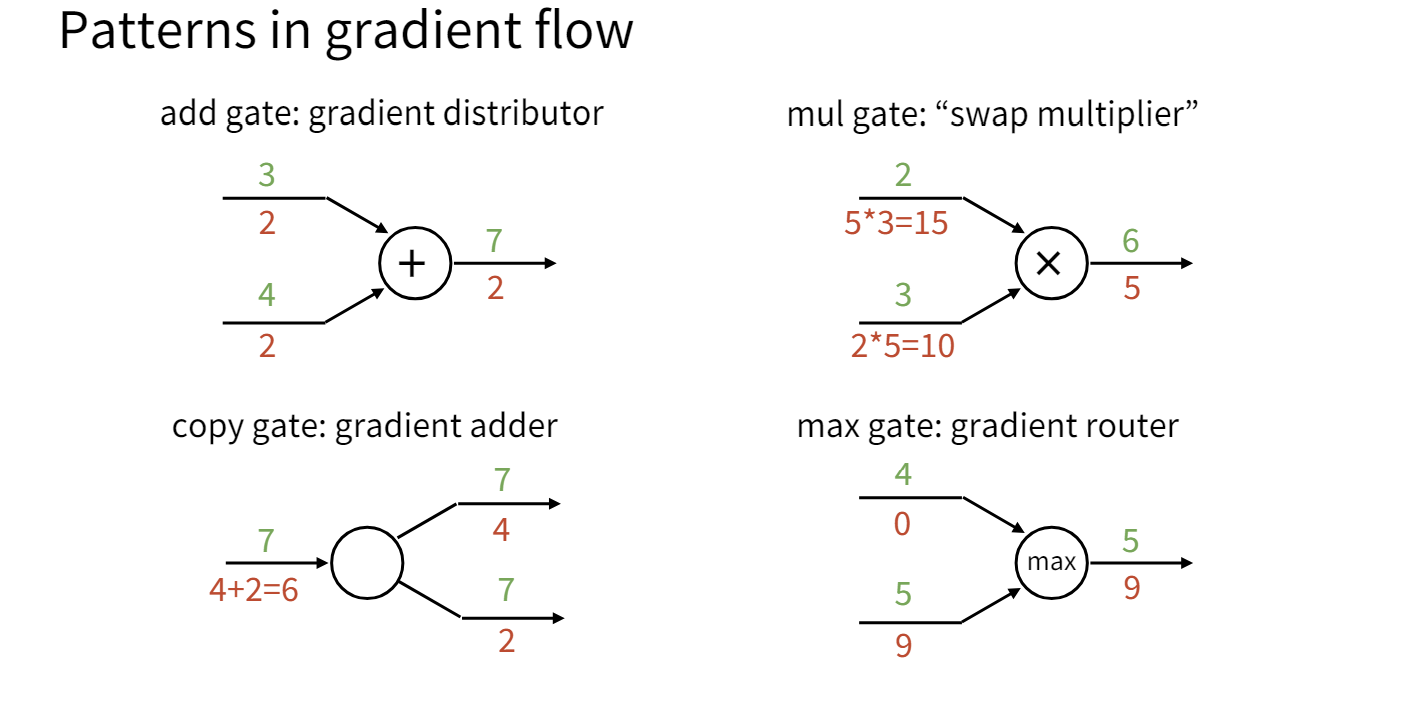
add gate：相加门将下游的梯度复制到上游的每一个输入。
copy gate：复制门将下游的梯度相加传到上游。copy gate和add gate在某种程度上是对偶的。
mul gate：乘法门将下游的梯度乘到上游并交换两个输入，mul gate在某种程度上将梯度混合在一起了。
max gate：最大门将梯度传播到最大的输入，相当于起到了一个路由的作用。

在神经网络中，我们实际上处理的不是标量，而是向量。道理是相同的，只需要将一元的求导变成对向量求导。整个计算过程是相通的。

这里的向量对标量求导很直观。而这里的向量对向量求导，实际上就是Jacobian矩阵（然而在实际的梯度计算中并不会显式地形成一个Jacobian矩阵）。

反向传播不仅能计算一阶的梯度，也能计算更高阶的导数。

Lecture 7

卷积层

在处理图像信息的时候，全连接层存在一个明显的局限性，全连接层会将一个32x32x3的图像，展开成一个3072维的向量，然后经过一个全连接的权矩阵 $W$ ，计算出输出。但是这样的问题是，图片中原有的位置信息全部丢失了。

卷积层可以解决这个问题。卷积层引入了卷积核，让卷积核在图片上滑动，然后计算卷积核覆盖的部分的带权和，输出到下一层。通过这种方式，卷积层保留了图片的空间信息。卷积核的大小一般是3x3或5x5。一个卷积层会包括不止一个卷积核，而是多个卷积核。

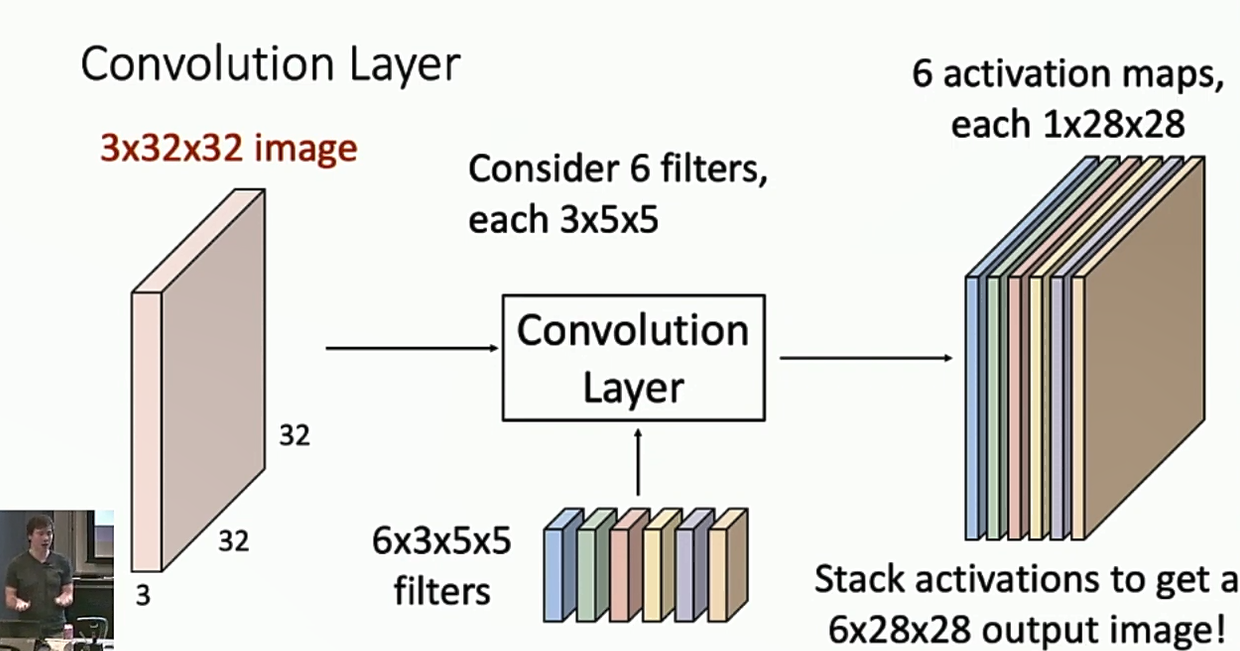
两种理解卷积层的视角：

将卷积层理解成activation maps，一种卷积核对应的输出的每一个位置告诉我们这个位置附近的像素和此卷积核的匹配程度。
将卷积层理解成一个特征向量的网格s每个位置有n种卷积核对应的输出，这些输出拼起来就是一个特征向量。

观察卷积层输出的形状，不难发现它也可以看作是图片，因此我们可以将卷积层相连，形成多层的卷积神经网络。

在连接卷积层的时候，记得一定要加上激活函数，原因和之前的全连接层s一样。如果不加激活函数，两个卷积层串联在一起，其实只是相当于一个卷积层的效果。

卷积核学习到什么？

回忆Lecture 3，在理解线性分类器的第二种视角里，我们发现线性分类器的权重实际上学习到了一种图片的“模版”，而卷积核学习到了什么呢？

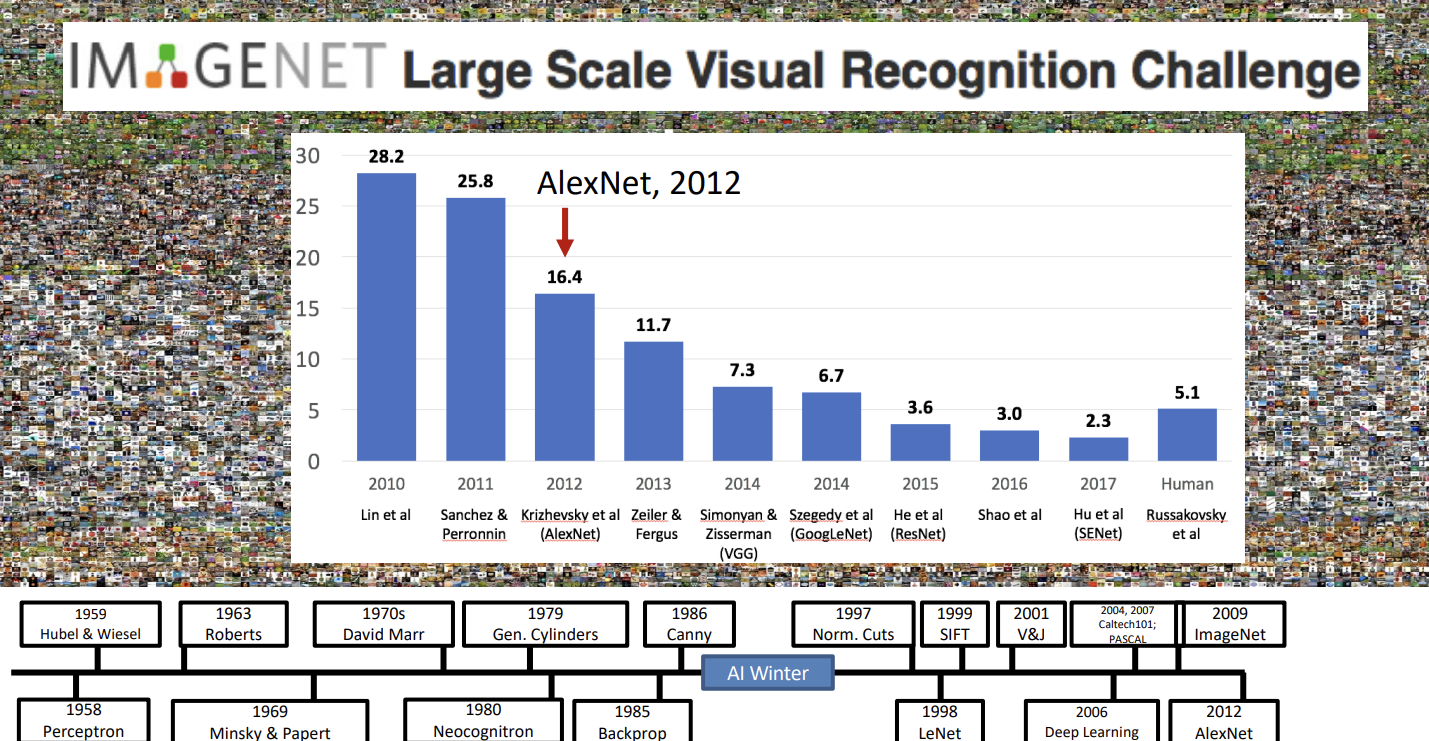
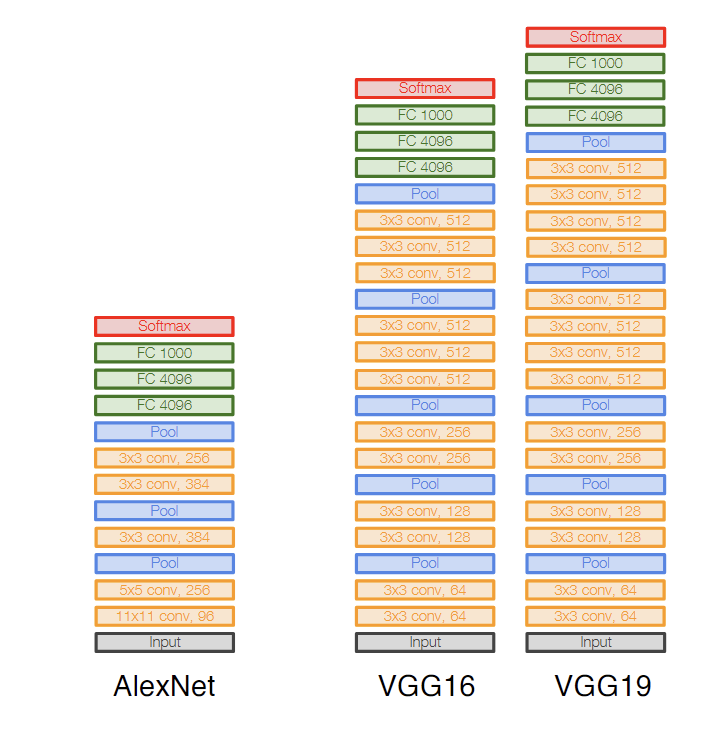
实际上，卷积核学习到的是一些局部的特征，如图，AlexNet的第一层是一些简单的条纹和网格纹理。

结合前面的两种视角，AlexNet第一层的输出，可以理解成图片对64种卷积核的激活地图，也可以理解成图片在每一个位置都有一个64维的特征向量。而这个输出会被AlexNet后面的卷积层使用，后面的卷积层可以利用前面学习到的简单的纹理，并组合它们形成更加复杂的pattern。

卷积层的超参数

首先是我们前面就提到的

输入的大小： $W \times W$
卷积核的大小： $K \times K$

经过这样的一层卷积之后，图片的大小会变成 $W - K + 1$

引入Padding

注意到我们上面的卷积会使得输出的图像形状变小几个像素，我们通常不希望输出发生这样的变化，最好是保证输入输出的形状保持相同，因此我们可以在图片的四个边缘加上 $P$ 个像素，用“0”填充。

这样，输出的图像大小就是 $W - K + 1 + 2P$ ，当 $P = (K - 1) / 2$ 时，输入输出的形状保持一致，这被称为“same padding”，也是最常用的一种设定。

用“0”填充图片边缘会不会引入额外的信息？Justin Johnson提到，实际上，zero padding隐式地给图片引入了边缘的位置信息。有一些卷积核会通过边缘的“0”学习到如何识别图像边缘。这不好说是一种Bug还是Feature。

引入Stride

注意到，假如输入的图片很大，或者卷积核的尺寸很小，我们就需要更多的层数才能让某一点“看到”整张图片。如果我们能让图片的大小缩小一点，就可以加快这个“看到全局”的过程。

因此我们可以引入一个stride， $S$ 。当用卷积核遍历图片的时候，我们让卷积核每次移动的距离为 $S$ ，这样，输出图片的大小就会被大大缩小。

总结

超参数：

Input： $W$
Kernel： $K$
Padding： $P$
Stride: $S$

最终的输出为： $(W - K + 2P) / S + 1$ ，我们一般会调整参数让这个式子能挣除。

补充

有时候会有卷积核大小为1x1的时候，这种层可以看作是每一个像素形成一个全连接层，通过这种方式可以将每一个位置对应的特征向量降维，有时候也是很有用的。

其他维度的卷积。我们刚才讨论的都是2D卷积，实际上，也可以进行1D卷积，3D卷积等，道理是一样的。

PyTorch提供了开箱即用的卷积层torch.nn.Conv2d、torch.nn.Conv1d、torch.nn.Conv3d，只需要对超参数进行配置，就可以往神经网络里加入卷积层。

池化层

刚刚提到了可以用Stride > 1，构造一个downsample的卷积层。另一种downsample的方式是使用池化层。

池化层一个好处就是它没有任何需要学习的参数。

Max Pooling

就是对每个区域计算最大值。

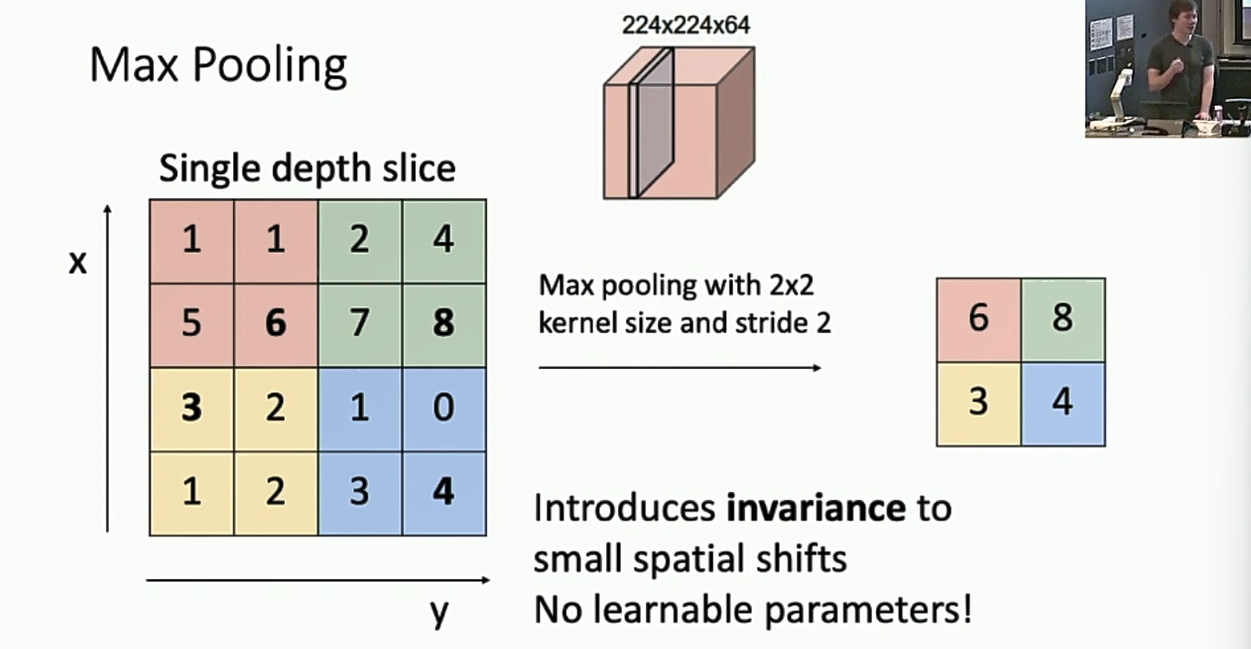
Average Pooling

就是对每个区域计算平均值。

搭建神经网络

有了卷积层、池化层这些乐高积木，我们就可以搭建自己的卷积神经网络了。卷积神经网络通常从前到后，图片的形状维度会越来越小，特征维度会越来越大，形成一个“逐渐铺平”的效果，CNN一个经典的结构是LeNet-5。

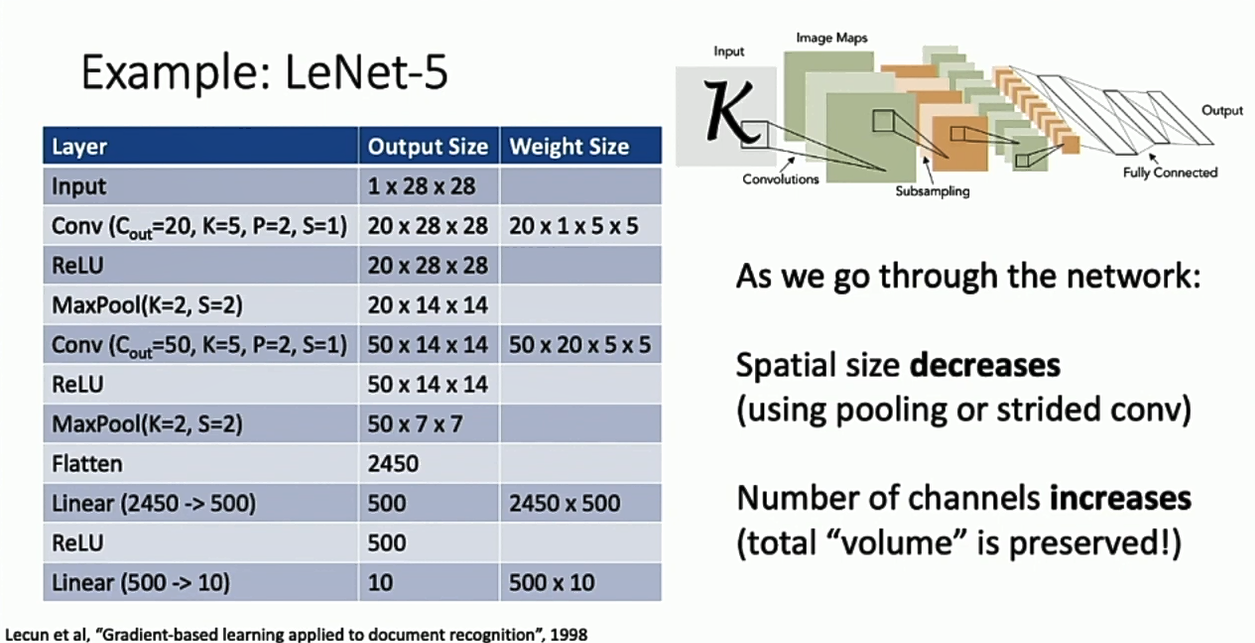
Batch Normalization

深度神经网络非常难以训练。

比起层数少的神经网络，深度神经网络非常难收敛。为了解决这个问题，我们引入normalizatio层。其中最常用的一种是batch normalization。

为什么normalization可以加速深度神经网络的收敛，我查阅了一些资料，以下是我的理解：

深度神经网络因为层数深，当训练的时候存在“内耗”的问题。因为误差反向传播到中间的某一层的时候，实际上已经叠加了后面所有层的梯度，这一层不是在“配合”我们的正确输出，而是在“配合”之后的所有层。而这种误差会被放大，第i-1层会去拟合第i层，导致数据在流过深度神经网络的时候经历十分“曲折”的旅途，大部分时间不是为了拟合训练数据，而是为了相邻层之间的对齐，造成了一种“内耗”。

这种现象的一种表现就是“internel covariate shift”，由于神经网络深度比较深，在训练的过程中每一层可能会不再独立同分布，使得某一层需要适应新的输入分布，还可能会造成数值落入激活函数的饱和区，造成梯度消失。batch normalization让输出保持平均值为0，标准差为1的“正态分布”。缓解了这个问题。（这就是统计上常用的“白化”处理）

但是有时候，这个平均值为0，标准差为1的限制可能太过与严格，为了增加灵活性，增强模型的表达能力，我们可以学习一个scale $\gamma$ 和一个shift $\beta$ ,令 $y_{i,j} = \gamma_j x_{i,j} + \beta_j$ ，然后在每个minibatch里面调整这两个参数。不过这带来一个反直觉的问题，就是我们同一个batch里面的不同数据，会互相之间影响，并且在测试模型的时候，我们并没有所谓的minibatch给我们计算参数。

所以我们可以在测试的时候，把这两个参数直接设置成训练时参数的移动平均。这样还带来了一个好处。由于normalization layer是线性的，因此当参数均为常数的时候，这一层可以合并到上一层，这是zero overhead!

一般来说，batch normalization layer会放在fully-connected layer或convolution layer后面，激活函数的前面。

好处：更快收敛、更稳定的随机初始化、test-time zero overhead等。

坏处：暂未被理论很好地解释，在training和在testing表现不同。

Layer Normalization

以下非课程内容，为个人学习并补充。

近些年来，batch normalization变得越来越不流行。新的网络更多使用layer normalization。如transformer。

layer normalization实际上比batch normalization更简单，它只对每个样本进行归一化，不依赖batch size，而且laer normalization在测试与训练表现一致。

其他的Normalization方法：

Instance Normalization：对每个样本的每个通道独立进行归一化，适合处理图像数据中的风格和内容。
Group Normalization：将特征通道分成多个组，对每个组进行归一化处理，综合了 Batch Normalization 和 Layer Normalization 的优点，适合于小batch size 和高维数据。
Weight Normalization：对权重矩阵进行归一化，将权重分解为规范化的部分和非规范化的部分，可以加速训练过程，提高模型收敛速度，特别是在深层网络中。