CS231n/EECS598 学习笔记（一） Lecture 1-4

课程介绍

Deep Learning for Computer Vision是一门介绍深度学习在计算机视觉中的应用的课程，本课程中介绍了如何实现、训练和调试自己的神经网络，并详细展示了计算机视觉的前沿研究。课程中还包括一些训练和微调视觉识别任务网络的实用工程技巧。CS231n是斯坦福大学的版本，由于这门课程在网络上最新的版本是2017年比较早，因此我选择了教学大纲基本相同，但有额外扩充内容的另一门课程，密歇根大学的EECS498/598，这门课在网上公开的最新版本是FA2019。

http://cs231n.stanford.edu/schedule.html

课后作业答案

下面是我的作业解答链接

https://github.com/cyrus28214/EECS598-solutions

Lecture 1

对计算机视觉做了简单的引入，主要介绍了计算机视觉的发展历史。

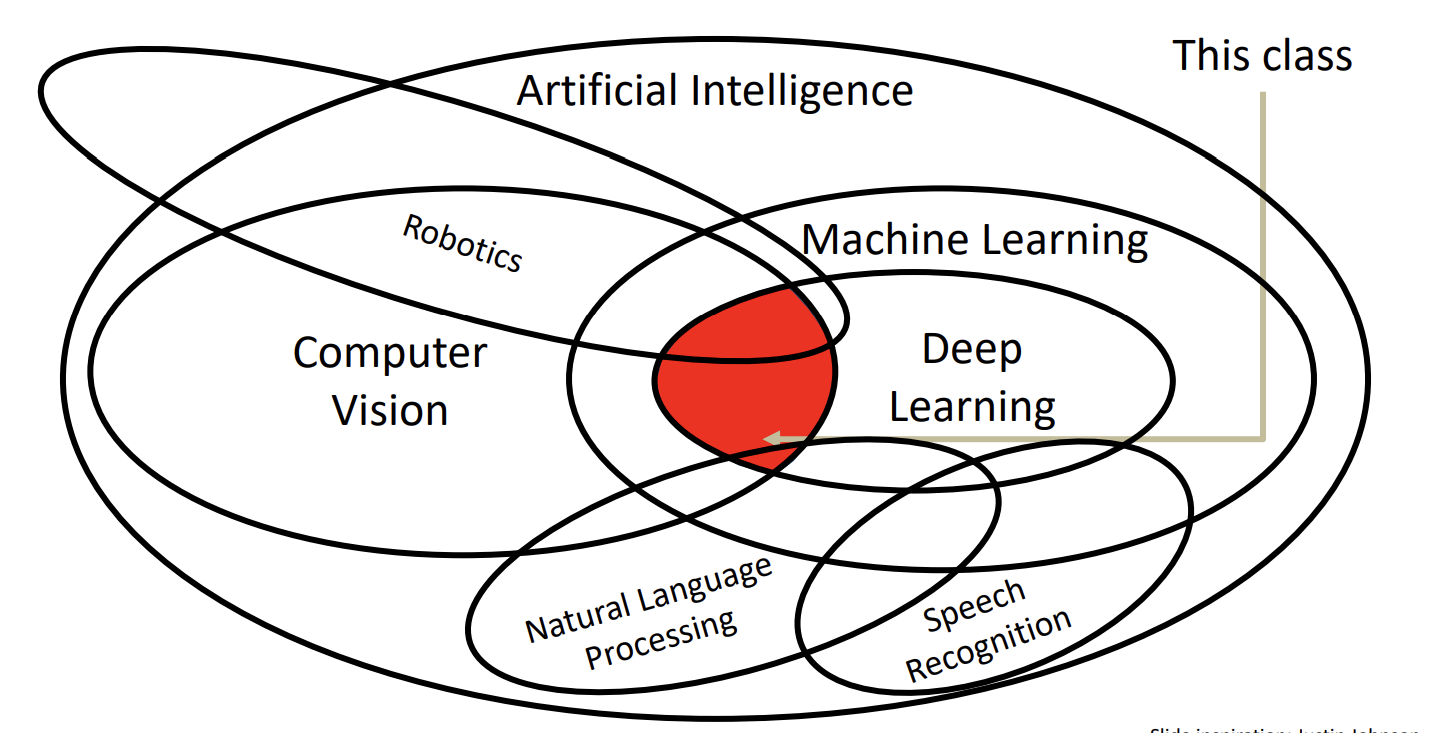
各种术语的范围辨析

这篇CV领域著名的论文SIFT完成了recognition in matching的任务。

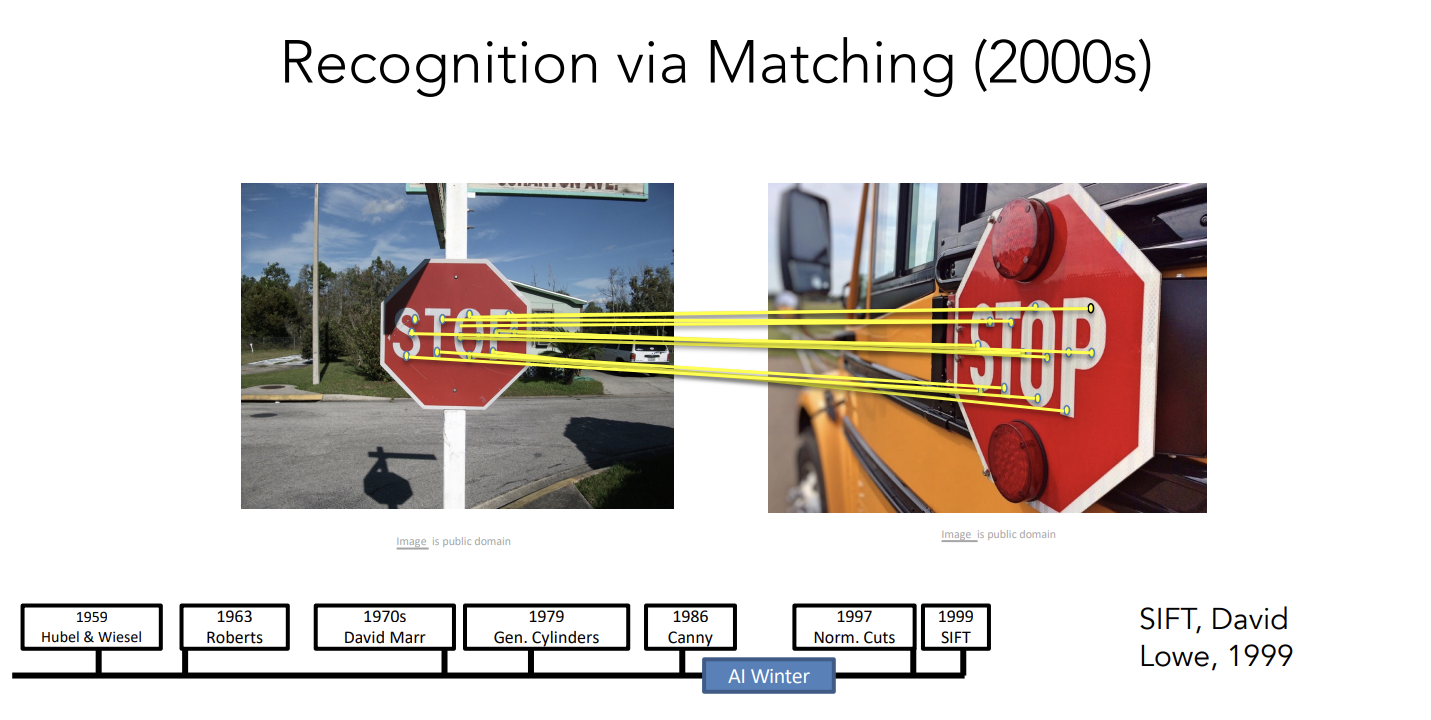
CV史上比较重要的突破，完成了matching的任务

人脸识别方面的技术得到了迅速的商业化。

人脸识别

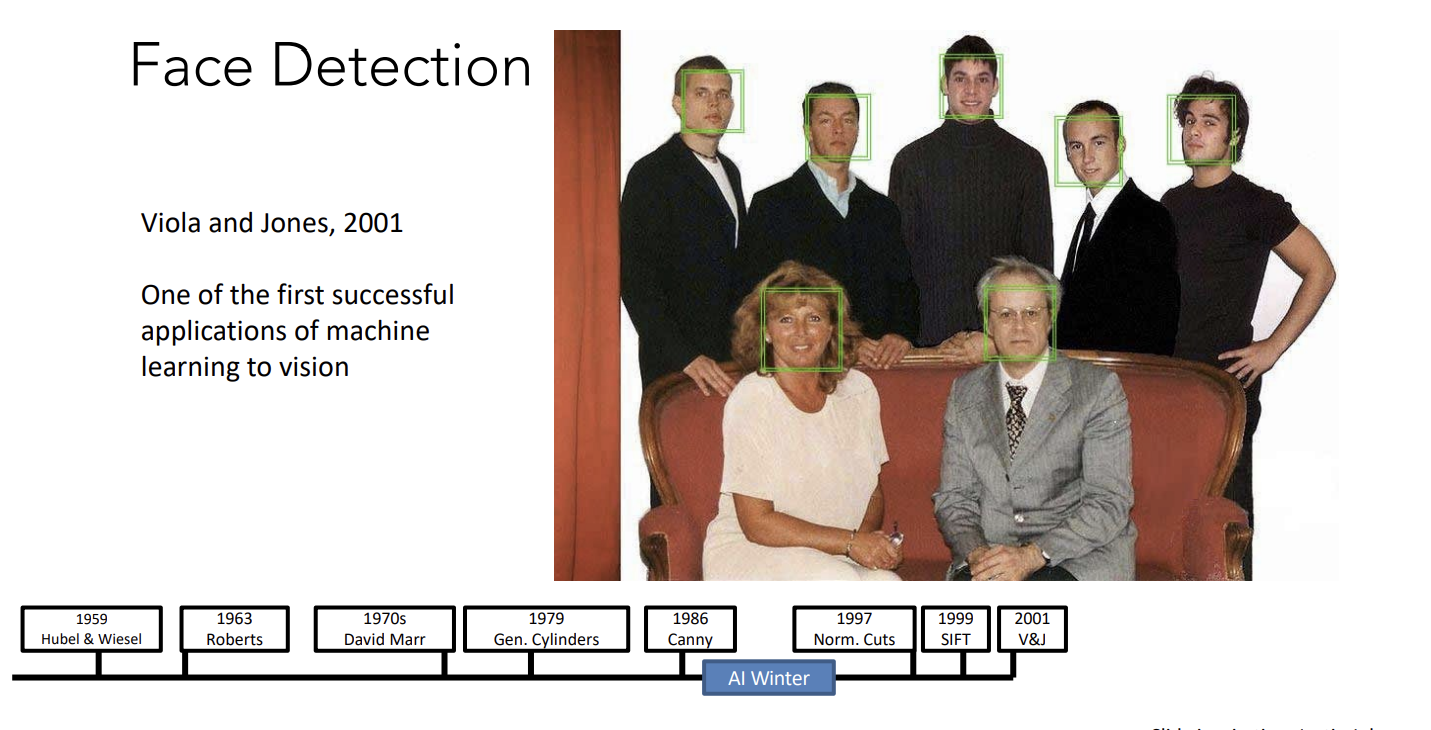
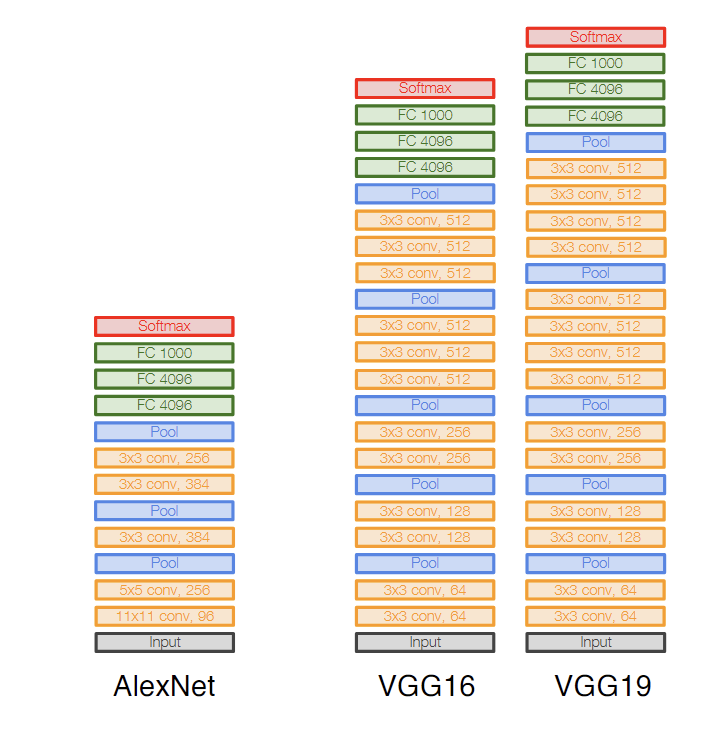
ImageNet项目作为一个图像数据集，其数据规模达到了惊人的1400万张图片，也成为了计算机视觉领域算法效果的重要检验标准。随后，AlexNet将深度学习引入计算机视觉领域，大大地降低了错误率，并开启了深度学习在CV领域的广泛应用。

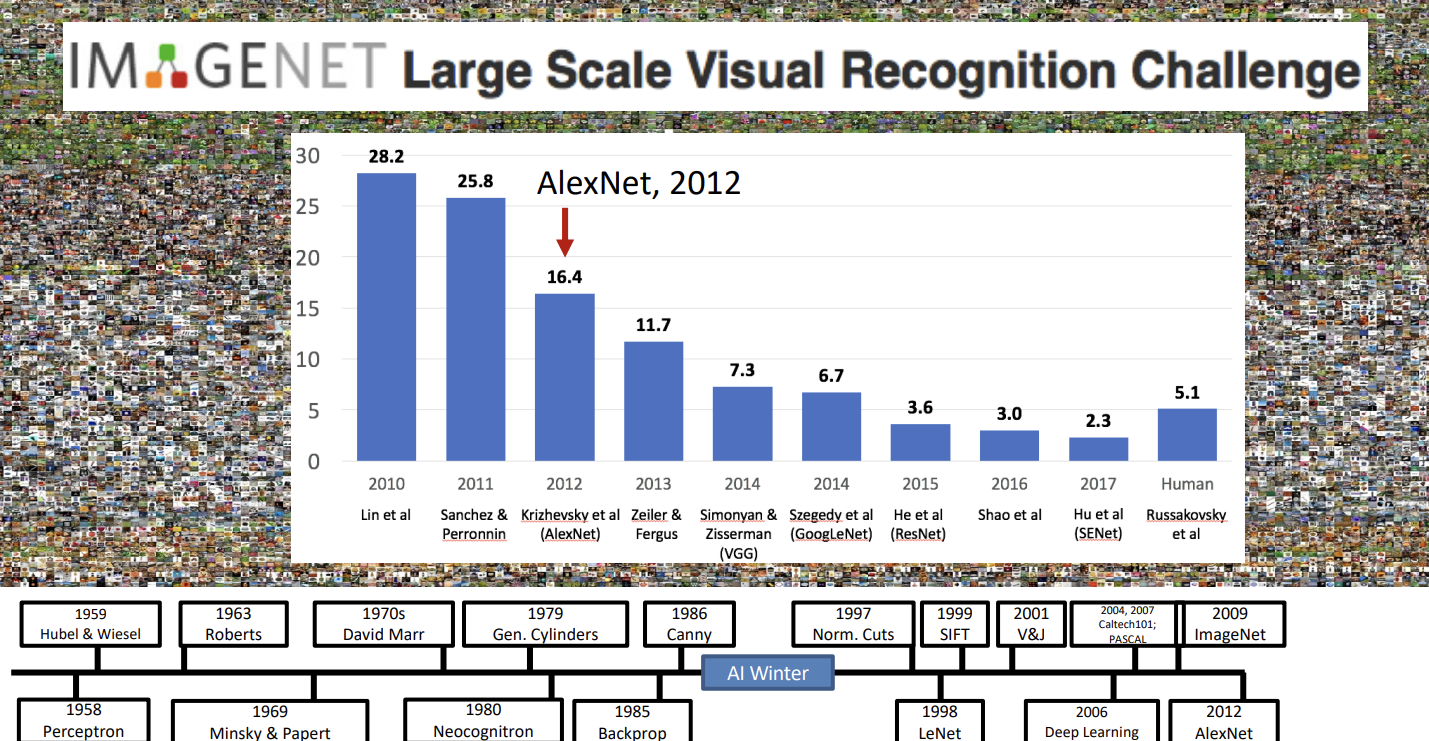
ImageNet & AlexNet

GPU的发展极大地增加了计算机视觉的计算能力。结合深度学习的模型，使计算机视觉领域得到突破。

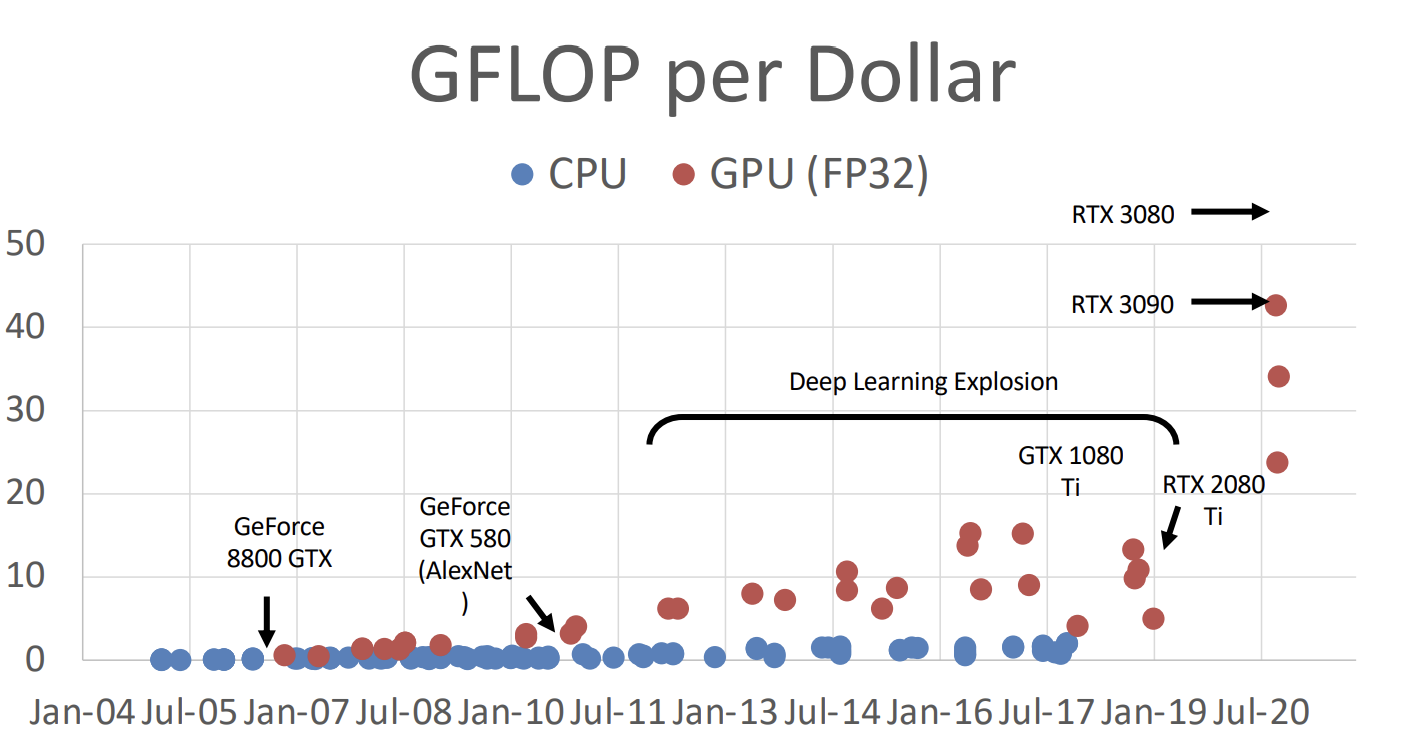
GPU的发展

Justin教授认为，计算机视觉领域的发展，主要取决于三个因素：算法、数据、计算。这三个方面对应上面提到的深度学习、ImageNet、GPU for deep learning。

三种因素

Lecture 1剩下的内容就是一些课程大纲的介绍，就不提了。

Lecture 2

Lecture 2首先使用了猫作为例子来阐述图片分类任务有哪些挑战，这个例子非常令人印象深刻，我看过的一些博客文章里，也引用了这个“CS231n的猫”的例子。

图片分类任务的挑战主要包括：

所谓的Semantic Gap，我看了一下，大致的意思就是说人类可以一眼看出来图片上是个猫，但是在计算机眼中，图片只是一堆数字组成的点阵，而且人类没法设计一个精确的算法告诉计算机什么是猫，怎么识别猫。
不同的视角：即使是同一只猫，在不同的视角下拍摄的图片也会大不相同。
光照：光照也可以是识别的对象发生很大的改变。
背景干扰：不同的背景可能会干扰模型的识别结果。
Occlusion：有时图片里的猫不会是一个完整的个体，而是有部分被遮挡了。
Deformation：物体会发生形变，譬如猫有不同的姿态，站着、躺着、坐着……
Intraclass variation：猫的品种不同，它们有不同的颜色、花纹、大小等。给计算机视任务造成了困难。
Context：比如说，猫可能与场景中的其他物体有关系，比如猫的身上有栏杆投下的影子，使得猫看起来像一只老虎，我们的算法甚至还需要理解现实世界的一些规律。

occlusion

deformation

context

要解决上面的问题，可以使用数据驱动（Data-Driven）的算法，这样你无需语义化地告诉计算机什么是猫，只需要提供大量的猫的图片，让计算机自己学习什么是猫。

这种方法同时带来了另一个好处：可重用，也就是说，你使用猫的图片训练模型，模型就能识别猫，使用星系的图片训练模型，模型就能分辨星系的种类。你无需为各种计算机视觉任务开发不同的模型。

data-driven

KNN算法（K-Nearest Neighbor Classifier）

KNN算法是一种非常简单的数据驱动算法，它非常容易实现。KNN并不是一个进行图像分类的理想算法（但是经常和其他算法结合，达到更好的效果），课程使用KNN应该是为了以此为例，解释数据驱动的算法。

KNN的基本思想是：我们首先将训练的图片保存在模型中。给定一张新的图片，我们首先计算这张图片与所有训练图片的距离，然后选择距离最近的K张图片，这K张图片中，出现次数最多的类别，就是这张图片的类别。

要计算图片之间的距离，首先你要把图片变成一个一维向量，比如一张(H, W, C)的图片（H、W、C分别代表高度、宽度、通道），就可以变成一个(H*W*C)的向量。然后，我们就可以计算任意两张图片之间的距离了。

距离函数有多种选择，如L1距离（曼哈顿距离）、L2距离（欧式距离）。公式如下：

$\begin{align*} d_1(I_1, I_2) &= \sum\limits_p |I_1^p - I_2^p| \\ d_2(I_1, I_2) &= \sqrt{\sum\limits_p (I_1^p - I_2^p)^2} \end{align*}$

从图中可以发现，L1距离实现的KNN算法的特点是决策边界都是横线、竖线或45°斜线，而L2距离实现的KNN算法的决策边界可以是任何直线。

knn

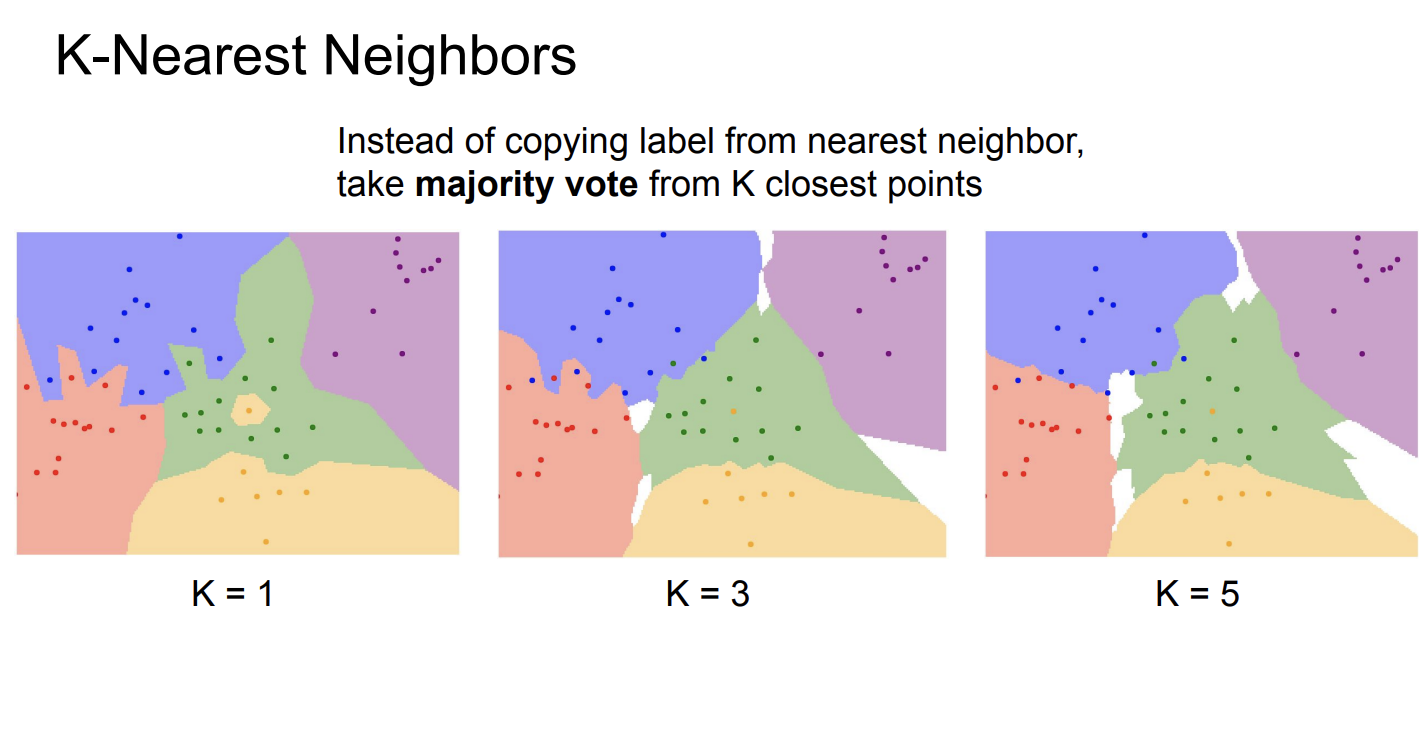
像 $k$ 这样，不是通过模型训练得到，而是提前设置好的参数，被称为超参数（Hyperparameter）。

训练集和测试集（Training Set and Testing Set）

训练集和测试集是两个非常重要的概念。训练集用于训练模型，测试集用于评估模型的性能。

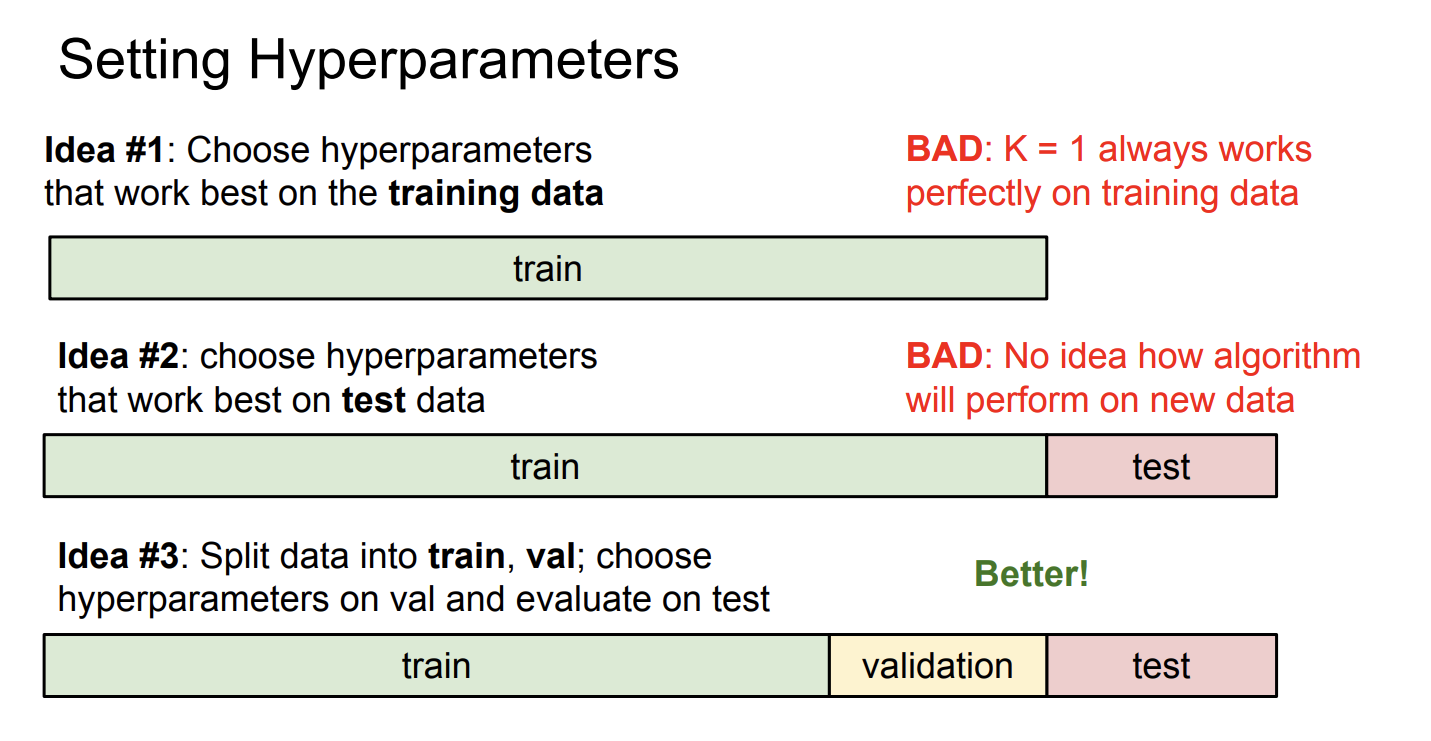
为什么要分训练集和测试集呢，因为你的模型有可能在训练集上表现很好，但是在测试集上表现不好，这种现象被称为过拟合（Overfitting）。

假如你将所有数据都作为训练集，那么你将无法评估你的模型到底在从未见过的数据集上表现如何。

具体到KNN算法来说，假如你选取 $k=1$ ，并使用同一份数据进行训练和测试，那么结果会怎么样？

答案是你的模型将永远是100%正确，你无法评估模型的效果如何。

交叉验证（Cross Validation）

交叉验证是用来评估模型性能的常用方法。将数据集分成n份，每次选择其中一份作为验证集（Validation set），其他n-1份作为训练集，然后训练模型，最后在测试集上模型的性能。交叉验证可以防止因为分割数据方式不同引起的误差。

设置超参数

KNN中有一个参数 $k$ ，代表选择最近邻的个数。 $k$ 的取值不同，KNN算法的效果也不同。

我们可以用交叉验证来设置超参数 $k$ ，我们不能故意选择一个使得模型在测试集上表现很好的 $k$ 。我们只能在最后使用测试集评估性能，不能人为地引入误差使得模型在测试集上表现很好。

在我们的KNN模型中，我们设置不同的 $k=1,2,3,\dots$ ，然后在验证集上测试模型的效果，得出了表现最好的 $k\approx 7$ ，然后用 $k=7$ 的模型在整个训练集上训练，最后用测试集评估结果。

用不同的距离函数实现的KNN算法

按照我的理解， $k$ 越小模型越倾向于过拟合，而 $k$ 过大的话模型容易欠拟合。

设置超参数

KNN的缺陷

图片之间的距离并不能很好的衡量图片的相似程度，比如只是对图片主体进行平移就会使图片距离变得很远。
计算的复杂性，课程中提到了Curse of dimensionality，假如我们在低维空间内使用足够多的数据点覆盖空间，KNN算法的确能得到不错的效果，然而随着模型维度的升高，我们需要的数据点个数将以指数增加。图像识别任务通常需要使用非常高（成千上万）个维度。假如我们使用 $4$ 个点覆盖一维坐标轴，那么要达到相似的数据密度，一个平面就需要 $4^2$ 个点，一个 $10000$ 维的空间就需要 $4^{10000}$ 个点！这是无法接受的
KNN的训练很快而计算很慢，KNN的训练只需要保存所有数据，如果按照传递引用算就是 $O(1)$ ，而计算新的数据的分类需要计算它与所有点的距离，这是 $O(ND)$ 的（ $N$ 是训练数据个数， $D$ 是维度）。这与我们的希望相反，我们更偏爱训练慢而计算快的模型（下一节课就会有这种模型）。

Lecture 3

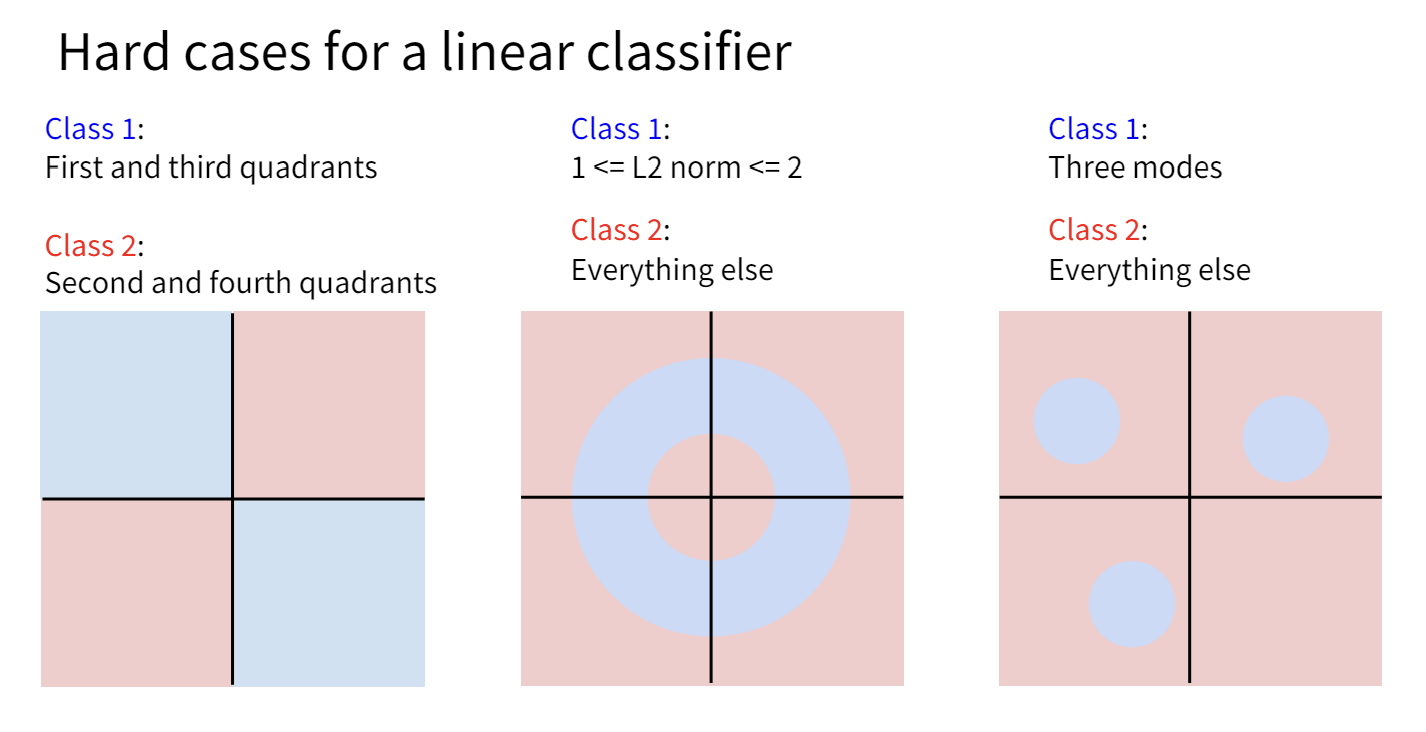
线性分类器

这节课介绍了一个新的模型：线性分类器（Linear Classifier）。

线性分类器就是这样一个简单的模型：

$f(x, W) = Wx$

其中 $W$ 是一个权重矩阵， $x$ 是输入的图片。

这个模型重要不是因为它效果很好，而是因为这个简单的模型是完成后续的复杂模型的“积木”。

为了理解这个重要的模型，这节课提供了三种视角：

三种视角

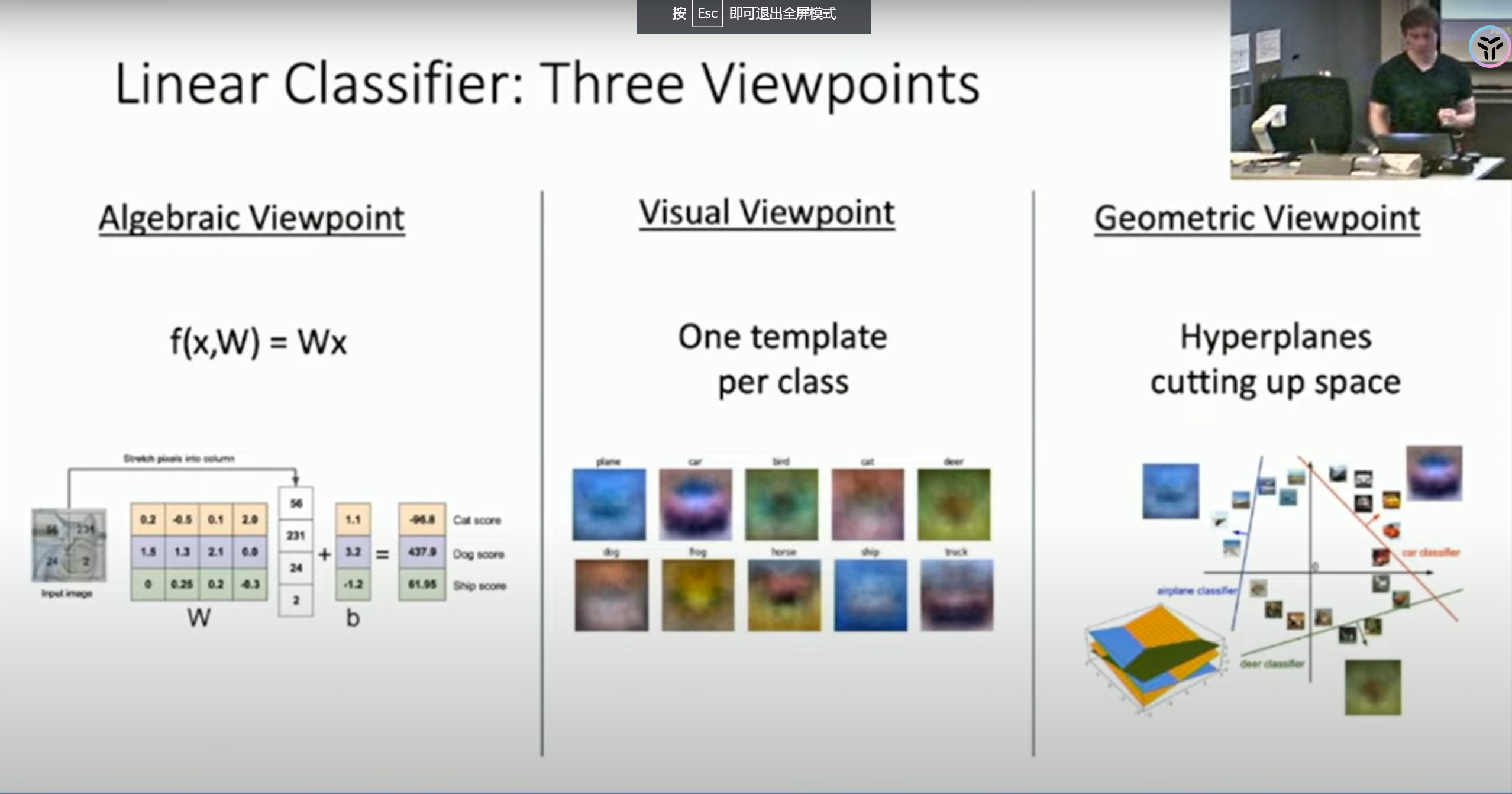
代数视角

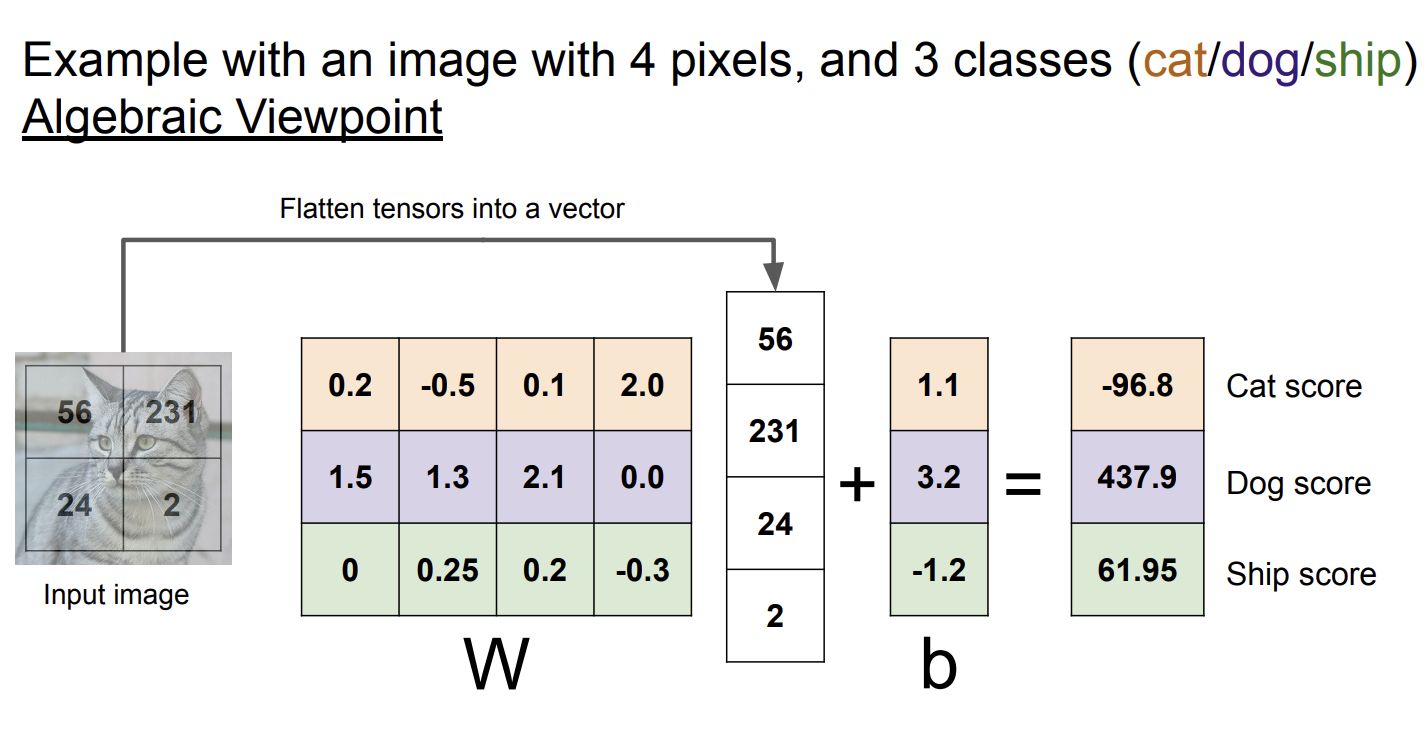
从代数视角看，线性分类器仅仅是把图片乘以一个矩阵 $W$ ，然后加上一个偏置项 $b$ ，一切操作都是线性的，这意味着将图片乘以一个常数，结果也将线性地变化。对于分类图片，这个性质比较奇怪，但是明白这个有利于我们更好地理解线性分类器。

可视化视角

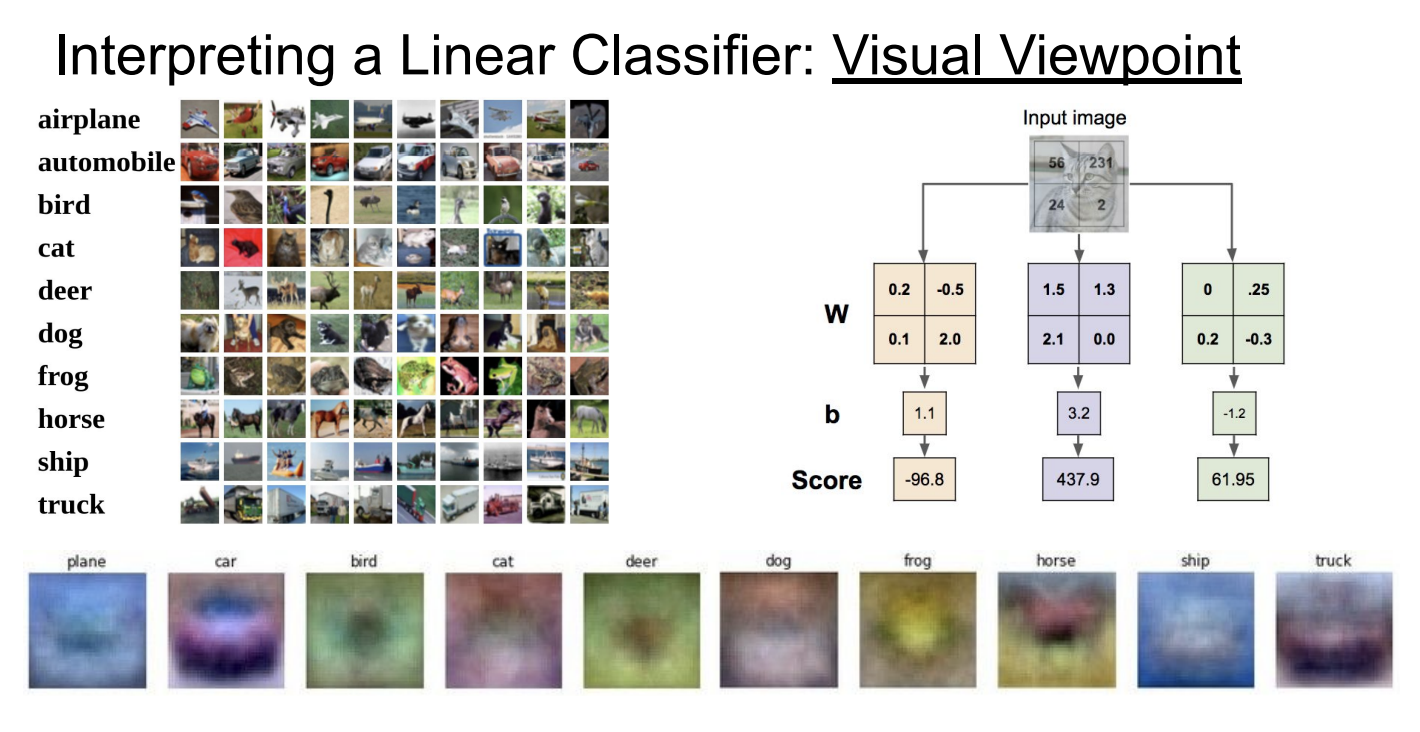
从可视化的视角来看，每一种类别都对应着一个不同的“模版”，我们可以把图片投影到这些模版上，和模版越接近的就会被分到相应的类别。

几何视角

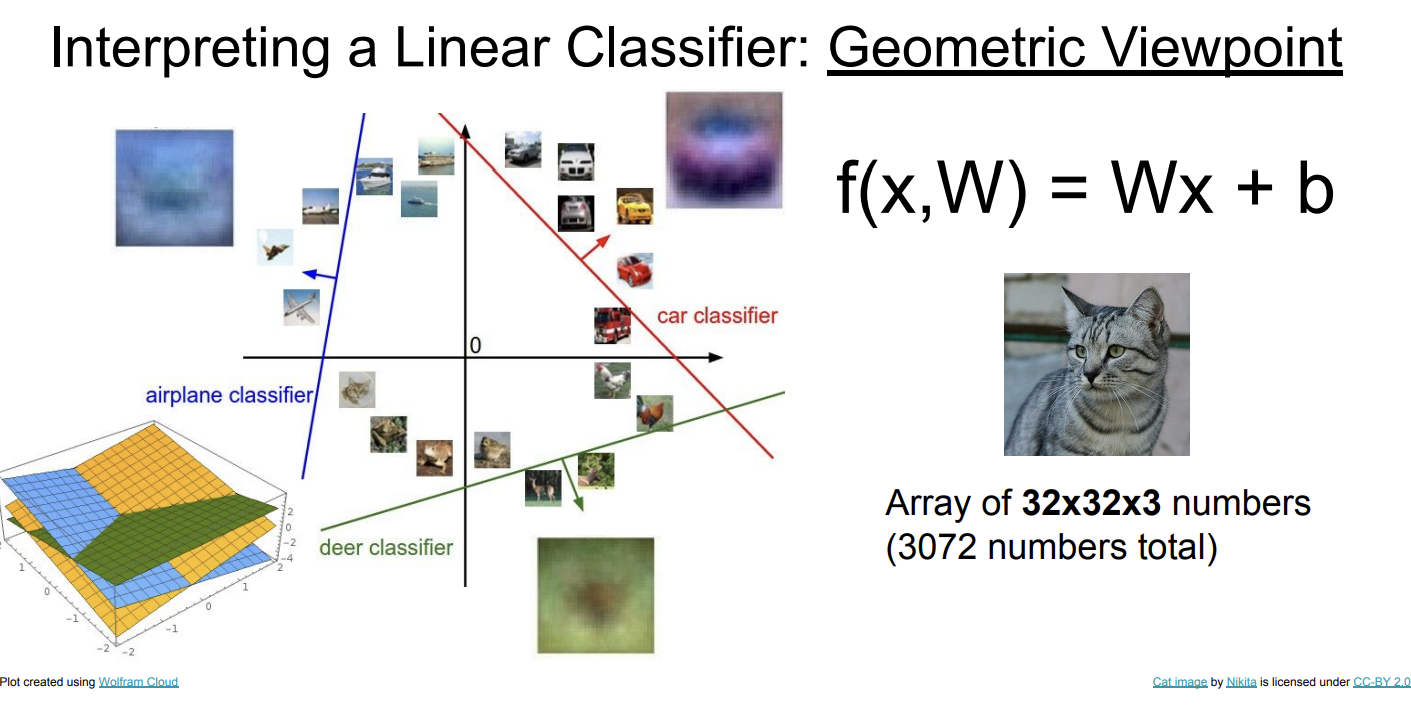
从几何的视角来看，线性分类器就是一个超平面，面向超平面的方向越往前就越属于某个类别。

损失函数

损失函数（Loss Function）是衡量模型预测结果与真实结果的差距的函数。损失越低，意味着模型的预测效果越好。

SVM Loss

SVM Loss会惩罚错误的分类，和不自信的正确分类。

$L_i = \sum_{j\neq y_i} \max(0, s_j - s_{y_i} + 1)$

总的Loss是所有 $L_i$ 之和

正则化（Regularization）

正则化可以防止过拟合。正则化向损失函数中加入一个正则化项，惩罚模型中过大的参数：

$L(W) = \frac{1}{N} \sum_{i=1}^N L_i + \lambda R(W)$

其中 $R(W)$ 是正则化项， $\lambda$ 是正则化系数。

L2正则化：

$R(W) = \sum_{i,j} W_{i,j}^2$

L1正则化：

$R(W) = \sum_{i,j} |W_{i,j}|$

Elastic Net：结合使用L1和L2正则化：

$R(W) = \sum_{i,j} \beta W_{i,j}^2 + |W_{i,j}|$

更多方案包括Dropout、Batch Normalization等。

正则化更喜欢简单的模型， $W$ 里面如果有绝对值很大的系数， $R(W)$ 就会变大，这使得模型在获得更好的表现的同时采用更简单的方法，避免了过拟合。

交叉熵（Cross Entropy）

交叉熵将模型的预测结果转换为概率分布，然后计算真实结果的对数似然。

$P(Y=k|X=x_i) = \frac{e^{f(x_i, W)}}{\sum_{j=1} e^{f(x_j, W)}}$

$L_i = -\log P(Y=y_i|X=x_i)$

Lecture 4

优化

优化（Optimization）是指找到使得损失函数尽量小的模型参数。

$W^* = \arg_W \min L(W)$

梯度下降

如果把损失函数看作是一座山脉，如果你要下山，你会每次都沿着高度降低的方向走，这就是梯度下降的思想。

梯度下降法计算出损失函数在当前参数的梯度，然后沿着负梯度的方向走一小步，然后更新当前参数，重复这个过程。

这里写的是负梯度而不是梯度，是因为数学上，梯度的定义是

$\nabla f(\boldsymbol{x}) = \left(\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \dots, \frac{\partial f}{\partial x_n}\right)$

这是一个矢量，矢量的方向指向 $f$ 函数增长最快的方向，而反过来，负梯度的方向就是 $f$ 函数减小最快的方向。

数值方法和分析方法

为了精度和效率的考虑，我们应该使用analytic的方法而不是numerical的方法来计算梯度。像PyTorch这样的深度学习框架都有Autograd的功能，可以方便地自动计算梯度，但有时你也需要手写梯度计算的代码。

Numerical gradient精度又低计算速度又慢，最好不要使用。例外是gradient check，你可以用数值的方法来验证analytic梯度计算的正确性。这个也不需要你手写，torch.autograd.gradcheck专门用来干这个。

学习率

学习率（Learning Rate）是梯度下降法中一个重要的超参数。学习率决定了模型参数更新的步长，如果学习率过大，模型可能无法收敛到最优解，如果学习率过小，模型收敛速度会很慢。

我们上面提到，梯度下降法就是每次向负梯度的方向走一小步，学习率决定了这一步有多长。

$W^* = W - \eta \nabla L(W)$

其中 $\eta$ 是学习率。在训练模型的时候我们会反复应用这一更新规则，直到损失函数下降到可以接受。

Batch

$\nabla L(W) = \frac{1}{N} \sum_{i=1}^N \nabla L(x_i, y_i, W) + \lambda \nabla R(W)$

$N$ 是我们训练集的大小，当 $N$ 比较小的时候，我们可以一次性计算所有梯度。但是当 $N$ 比较大的时候，一次性计算梯度会是比较昂贵的，（比如显存不够用之类的），这时我们可以分 batch计算梯度,每次只送入一部分数据计算梯度，然后更新参数。

这就引入了一个新的超参数batch_size。超参数越来越多了，终于有调参炼丹的感觉了（bushi

batch_size的参考取值差不多是32、64、128、256这个大小。

随机梯度下降（SGD）

随机梯度下降没什么难理解的，就是每次从训练集中随机sample一个batch来梯度下降。

SGD + Momentum

SGD有一些问题。

Zigzag

由于SGD每次选择梯度最低的方向，如果某个维度上梯度下降很快，那么其他维度上的步长就会很小，导致算法走出zigzag的形状。

关于图片底部这句话，想要理解它需要一定的线性代数基础，如果不懂的话跳过也没关系。

Aside: Loss function has high condition number: ratio of largest to smallest eigenvalue of Hessian matrix is large.

下面是我个人的一点理解：

Hessian矩阵可以类比成是一元函数的二阶导。直观理解的话，Hessian矩阵可以描述函数在某一点处弯曲的形状。

矩阵的条件数可以衡量矩阵有多“扁”，比如正交矩阵你就当做是一个圆，它每一个方向上都一样长，它的条件数是1。一个条件数很大的矩阵可以看成一个很扁的椭圆，它最显著的维度和最不显著的维度相差很大。

Hessian矩阵的条件数很大的话，说明loss funtion在某个维度上面呈现陡峭的“V”形，函数的梯度来回变化，导致算法走出zigzag的形状。

鞍点

鞍点（Saddle point）就是长这样的点：

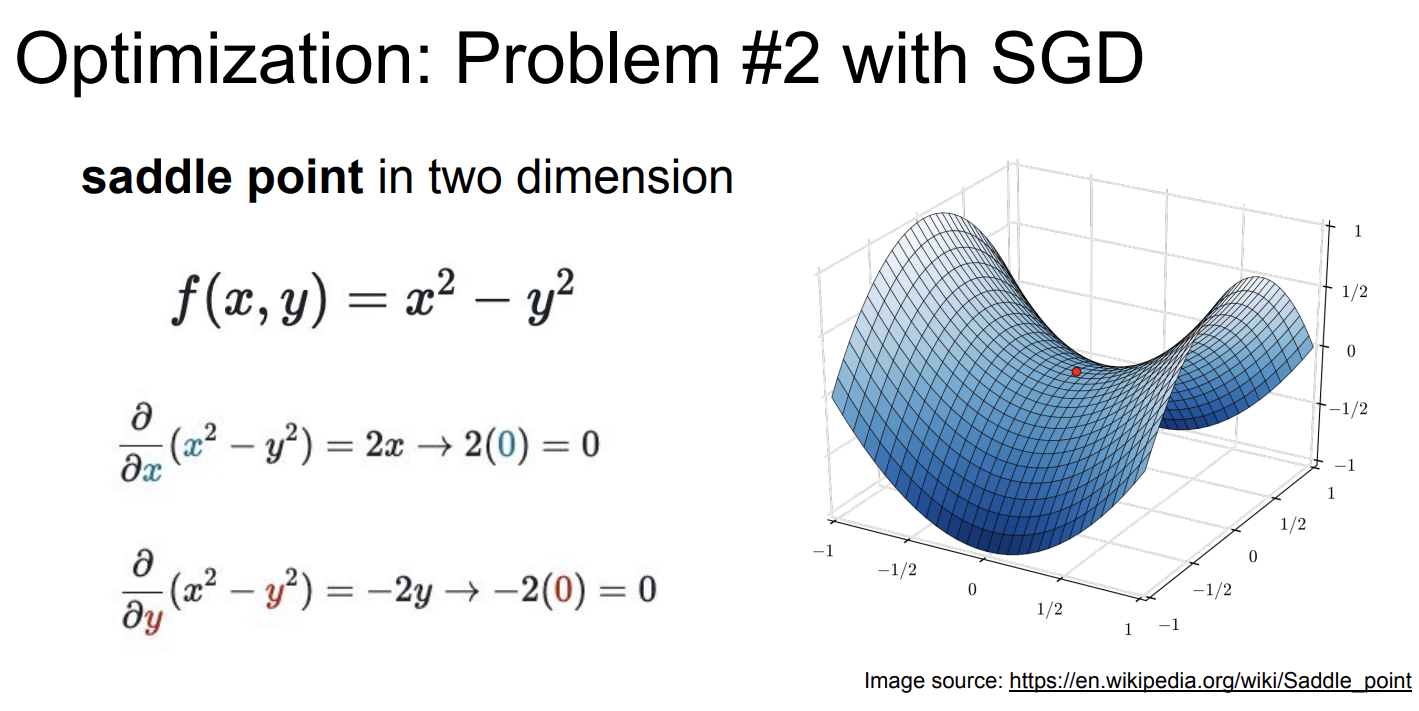
鞍点并不是极小值，但是鞍点的梯度却是0，按照之前的算法，零梯度会让我们卡在鞍点动不了。

顺带一提，Hessian矩阵也可以用来判断鞍点，如果 $\nabla f(\boldsymbol{x})=0$ ，且 $\mathbf{H}$ 是不定矩阵，即特征值有正有负，那么 $\boldsymbol{x}$ 就是鞍点。（当Hessian矩阵有零特征值的时候这个判断失效，需要展开到三阶或以上）

解决方案

这两个问题都可以通过引入动能项来解决。

$\begin{align*} v_{t+1} &= \rho v_t - \alpha \nabla L(x_t)\\ x_{t+1} &= x_t + v_{t+1} \end{align*}$

这个方程有很多种写法，如果见到了不一样的形式不用奇怪，都是对的

$v$ 就好像给了这个点一个速度，让它记住历史的梯度， $\rho$ 用来模拟摩擦，让速度衰减，然后每次用梯度更新速度，再用速度更新参数。

引入动能项可以解决zigzag问题，因为两个相反方向上的梯度会在动能项里相互抵消，让模型专注于其他维度。

也可以解决鞍点问题，模型走到鞍点的时候还有动能，不会停滞不前。

一举两得！

Nestrov Momentum

Mestrov Momentum是SGD + Momentum的变种，它用了“look ahead”的思想，使用 $x_t+\rho v_t$ 而非 $x_t$ 处的梯度。

$\begin{align*} v_{t+1} &= \rho v_t - \alpha \nabla L(x_t + \rho v_t)\\ x_{t+1} &= x_t + v_{t+1} \end{align*}$

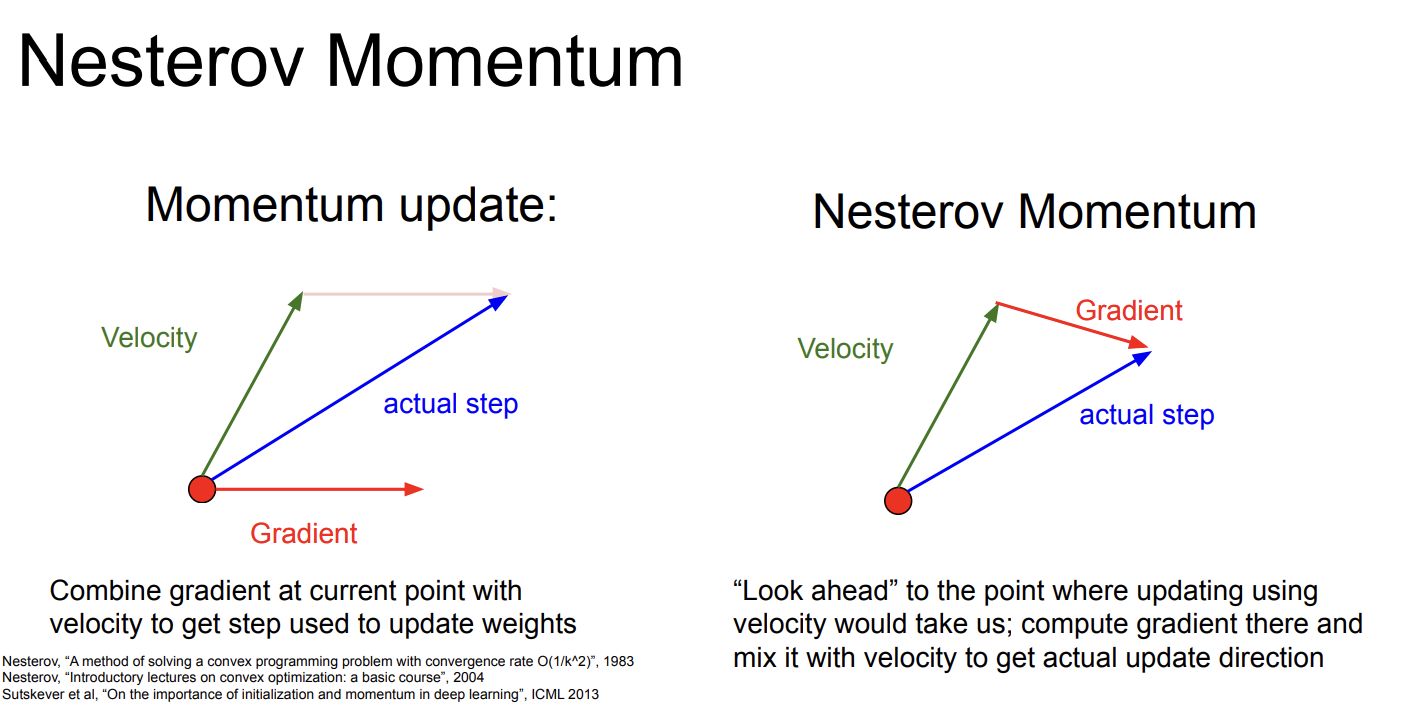
关于这个算法我查阅了相关资料，之所以这样做有更好的效果，是因为这种做法会包含函数的二阶项，允许更加精细的梯度下降（但不是真正的二阶近似）。具体的数学推导比较冗长，有兴趣可以自行了解。

Adagrad

Adagrad是一种自适应学习率的方法，它会动态调整学习率。当梯度比较平坦的时候走得快一点，梯度比较陡峭的时候走得慢一点。

RMSprop

RMSprop是Adagrad的变种，增加了Decay。

Adam

Adam≈RMSprop + Momentum。Adam是实践中非常常用，效果也很不错的Optimizer。

L-BFGS

到目前为止我们的优化算法都是一阶近似，而BFGS算法使用了二阶近似，当一次性使用整个训练集做full batch的时候效果非常好，但是当使用mini-batch的时候效果不怎么好。这比较好理解，因为用到了二阶项，如果batch太小的话，高阶项比低阶项更容易出现偏差。

缺点是复杂度是 $O(n^3)$ 的，一般只用于小数据集。

L-BFGS是BFGS的内存优化版本。

In practice

Adam是一个很好的默认选择，在大多数情况下效果不错。
SGD + Momentum有时比Adam好，但是需要很多玄学调参。
如果训练集比较小，你的机器能跑 $O(n^3)$ ，试试L-BFGS吧。