博客新添加了搜索功能
随着写的博文越来越多。博客也急需一个搜索工具,我使用的Hexo主题NexT刚好对 local search 功能有比较好的支持,就简单配置了一下,添加了搜索功能。
如果你之前访问过我的博客,浏览器可能缓存了旧版的CSS文件,旧版的CSS文件没有搜索功能所需要的样式,搜索功能可能会出现排版错误。只需要按Ctrl+F5强制刷新缓存即可恢复正常(Chrome下是这个快捷键,其他浏览器没有试过)。移动端浏览器如果没有强制刷新缓存的功能,清除浏览器缓存即可。
费马小定理和欧拉定理
费马小定理
定义
若 ppp 是素数,且 gcd(a,p)=1\gcd(a,p) = 1gcd(a,p)=1 ,则
ap−1≡1(modp)a^{p-1} \equiv 1 \pmod{p}
ap−1≡1(modp)
另一种形式:若 ppp 是素数,则
ap≡a(modp)a^p \equiv a \pmod{p}
ap≡a(modp)
证明
构造集合 A={1,2,…,p−1}A=\{1,2,\dots,p-1\}A={1,2,…,p−1} ,将集合中每一个数都乘以 aaa 再模 ppp ,即 rn=n×a mod pr_n=n\times a \bmod prn=n×amodp ,得到新集合 B={r1,r2,r3,…,rp−1}B=\{r_1,r_2,r_3,\dots,r_{p-1}\}B={r1,r2,r3,…,rp−1} 。
则有 A=BA = BA=B ,这是因为 ∀x,y∈A, x≠y\forall x,y \in A, \; x \neq y∀x,y∈A,x=y ,有 ax−ay=a(x−y)≢0(modp)ax-ay=a(x-y)\not\eq ...
SQL学习笔记(九)在Python中使用SQL
SQL很少被单独使用,通常SQL会与其他的一些语言结合使用,比如Python、Java、 C#等等。这篇文章里,我们关注如何在Python中使用SQL操作数据库。
Python中内置了SQLite3,你只需要执行
1import sqlite3
就可以开始使用了,不需要安装任何第三方库。
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758db = sqlite3.connect("database.db") # 连接到一个现有的数据库,如果没有这个文件就创建它cur = db.cursor() # 创建一个cursor,才能执行SQL语句# cur.execute(你想执行的SQL语句)cur.execute("CREATE TABLE books ('title' TEXT NOT NULL, 'price' REAL, 'sales ...
Linux中的三种时间戳:atime、mtime、ctime
标准的 POSIX 文件有三个时间戳:
简称
全称
含义
atime
access timestamp
最后一次读取的时间
mtime
modification timestamp
最后一次写入的时间戳
ctime
status change timestamp
最后一次更改文件元信息的时间戳
这里面的atime和mtime很好理解,分别对应了读取和写入文件,但是ctime就比较不好理解了。
文件元信息是关于文件本身的信息,比如文件的大小、权限许可、所有者这些,不在文件的内容里的信息。比如修改文件的访问权限的时候,atime和mtime都不会改变,但是ctime会改变。
要查看文件的元信息,包括(atime、mtime、ctime)可以使用stat。
12345678910cyrus:~$ touch new_filecyrus:~$ stat new_file File: new_file Size: 0 Blocks: 0 IO Block: 4096 regular empty fileDevice ...
ZJU校巴-calculator解题记录
题目
给了一个IP和端口,提示使用netcat连接:
1nc 10.214.160.13 11002
连接后显示以下文本
12345678================================================Mom: finish these 10 super simple calculations, and you will get a flagMelody: that's easy...Mom: yep, in 10 seconds================================================1941304599 + 1278737850 + 446307018 + 197487298 + 305703907 + 1425271161 - 806389023 + 1991017585 - 490014616 + 1353220023 =
分析
只有10秒的时间要完成10题,显然要编程来完成。但是先尝试一下手动输入答案,把上面的式子拷到Python REPL里,再把答案拷回去,显示“Good, next ...
SymPy学习笔记(七)矩阵
Matrix()可以创建矩阵,参数是一个二维数组。如果传入了一维数组,默认会生成一个列向量。
与 SymPy 中的其他对象不同,Matrix 是可变的。这意味着它们可以就地修改。这样的缺点是 Matrix 不能用于需要不可变的地方,例如其他 SymPy 表达式内部或作为字典的键。要用不可变版本的 Matrix,可以使用 ImmutableMatrix。
shape(M)返回一个元组,描述了矩阵的形状。
.row(0)可以得到第一行,.col(-1)可以得到最后一列,负数下标倒序访问这一点和 Python 中的数组是一样的。
.col_del()和``.row_del()可以删除行或列。.row_insert和.col_insert`可以插入行或列。
1234567891011121314151617181920>>> M.col_del(0)>>> M⎡2 3⎤⎢ ⎥⎣0 4⎦>>> M.row_del(1)>>> M[2 3]>>> M[2 3]>>> M = ...
SymPy学习笔记(六)解方程
求解方程
在SymPy学习笔记(二)需要避免的坑中已经提到过,SymPy中表达相等应该用Eq()而不是==或=
用solveset(equation, x)可以求equation关于x的解集,如果等式右边是0,也可以不写成solveset(Eq(expr, 0), x),直接写成solveset(expr, x),例如:
1234>>> solveset(Eq(x**2, 1), x){-1, 1}>>> solveset(x**2 - 1, x){-1, 1}
如果无解,将返回 ∅\varnothing∅ ,如果无法求解,会返回一个条件集合。
1234>>> solveset(exp(x), x) # 无解∅>>> solveset(cos(x) - x, x) # 无法求解{x │ x ∊ ℂ ∧ (-x + cos(x) = 0)}
求解线性方程组
使用linsolve()
12345678>>> linsolve([x ...
SQL学习笔记(八)事务
“事务”的介绍
事务(Transaction) 可以将一系列数据库操作绑定在一起执行,要么一起成功,要么都不执行。
设想假如我去银行取钱,我的账户余额扣除了1000元,但是这个时候ATM机坏了,什么都没有吐出来,此时我的钱就凭空消失了。如果把“从账户里扣除1000元”和“ATM吐出1000元”绑定成一个 事务 ,就可以避免这种情况的发生,如果ATM吐钱失败了,我的账户也不会扣钱。
还有一种情况,是David教授在CS50的课上举的例子,假如宿舍里有一个小冰箱,一天我打开冰箱发现牛奶喝完了,于是我去买牛奶,这时我的室友回来了,他也看到冰箱里没牛奶了,于是也去买。结果两个人都买了牛奶,冰箱放不下了。
买牛奶这个问题的关键在于,我的室友并不知道冰箱有没有牛奶的状态正在从“没有”更新到“有”,他只能看到冰箱里“没有”牛奶,而不知道我已经去买牛奶了。具体到数据库上,我们需要一种方法,把数据库“锁住”,让其他读取操作等待,直到数据更新完毕后再执行。
“取钱”和“买牛奶”这两个问题都可以通过SQL中的“事务”来解决,你只需要把一系列的命令用BEGIN TRANSACTION和COMMIT包裹起来就可 ...
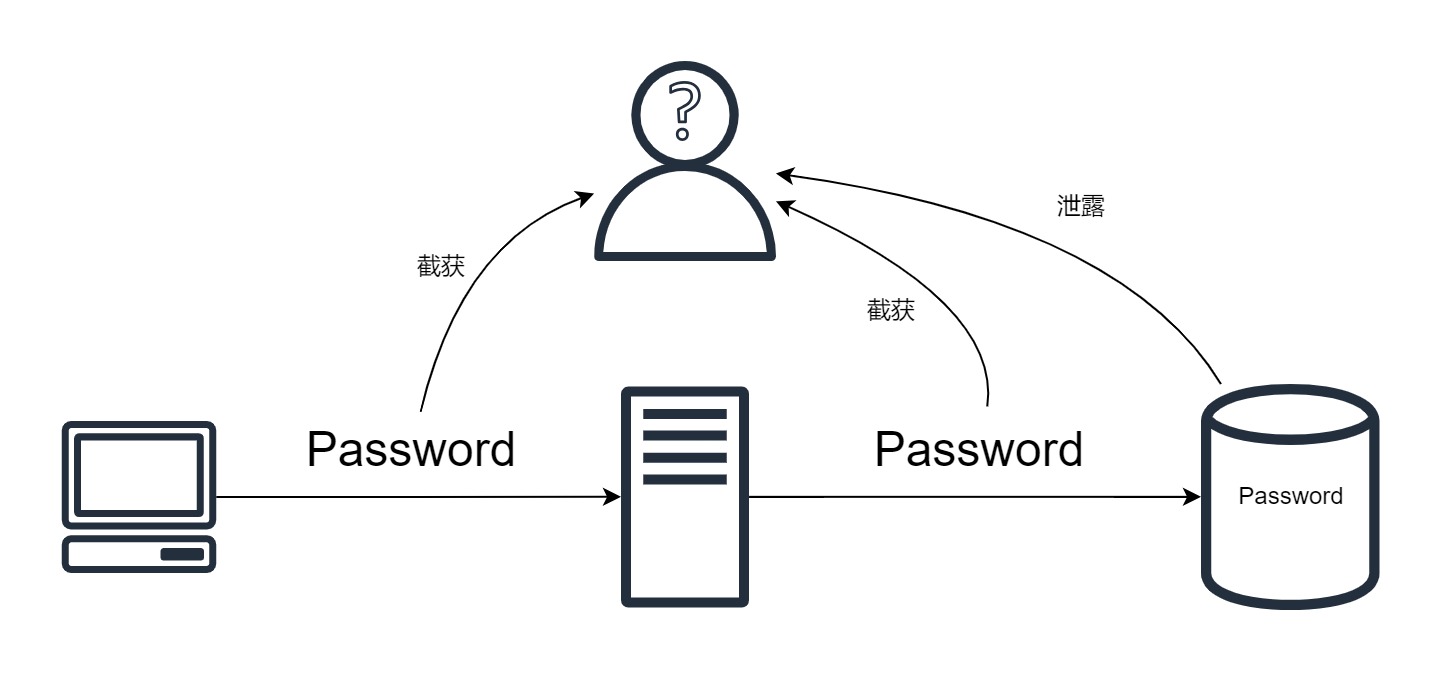
密码在数据库中的加密存储
简介
本文将从攻防两方的视角出发,简单讲解在数据库中储存密码的正确方法。
明文储存
我们都知道不应该在数据库中明文储存密码,假设有个粗心的程序员忘记了这一点怎么办呢?
有两种可能,攻击者可能可以在密码传递的过程中截取密码(假如传递的过程没有其他的保护),或者数据库泄露给了攻击者。
如果整个数据库都泄露了(拖库),情况非常糟糕,因为你的所有用户的密码都泄露了,你的所有用户数据都被开放给了攻击者,所有用户的身份认证都失效了!
储存哈希值
为了避免这一点,我们可以不储存明文密码,而是储存密码的哈希值Hash(Password)Hash(\text{Password})Hash(Password)。
一个理想的哈希加密函数需要满足这些条件:
一致性:对于相同的输出,输出应该是相同的, Hash(x)=Hash(x)Hash(x) = Hash(x)Hash(x)=Hash(x)
不可逆性:难以将哈希值还原成原始数据,即 Hash−1(Hash(x))=xHash^{-1}(Hash(x)) = xHash−1(Hash(x))=x 是难以计算的。
抗碰撞性:对于随机的 xxx 和 yyy ...
SymPy学习笔记(五)微积分
SymPy提供了完善的微积分支持:
求导
diff(expr, x)可以求expr关于x的导数,也可以写成expr.diff(x)。
diff(expr, x,x, x)可以对x求三阶导,也可以写成diff(expr, x,3)或expr.diff(x, 3)。
Derivative()可以创建一个导数但不计算它
对未计算的导数使用.doit()可以计算它。
积分
integrate(exp(-x), (x, 0, oo))将会计算
∫0∞e−x dx=1\int\limits_{0}^{\infty} e^{- x}\, dx = 1
0∫∞e−xdx=1
其中oo是两个“o”,用来表示无穷大。
integrate(exp(-x**2 - y**2), (x, -oo, oo), (y, -oo, oo))将会计算
∫−∞∞∫−∞∞e−x2−y2 dx dy=π\int\limits_{-\infty}^{\infty}\int\limits_{-\infty}^{\infty} e^{- x^{2} - y^{2}}\, dx\, dy = \pi
−∞∫∞−∞∫∞e−x ...