简介

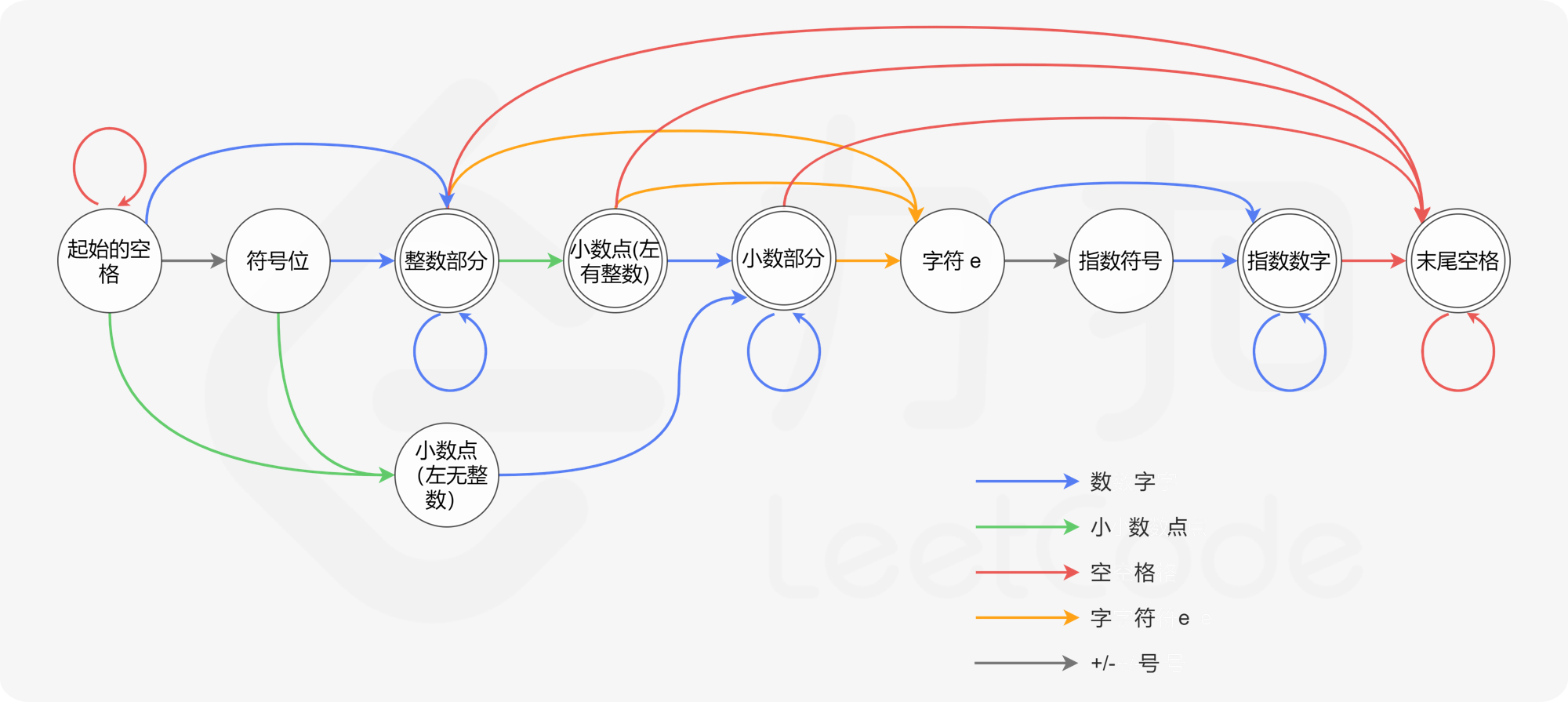
堆排序就是利用堆进行排序，如果对堆这种数据结构不熟悉可以看一看我的这篇文章。

堆排的思想很简单，就是在需要排序的数组上建立堆，然后执行pop操作，直到堆为空，因为每次pop出来的元素都是堆中的最大/最小值，所以可以保证出来的元素有序。堆排也是一种不稳定排序，时间复杂度O(nlog⁡n)O(n \log n)。堆排序相比于先前两种排序的优势是它不需要递归，堆排序使用了更少的栈空间，防止因递归层数过多引发的低效（尤其是对于快排来说）。

实现

只要实现了堆的代码，堆排就很简单了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
class Heap{
        inline int& _get(int node); //_get不能暴露给用户，因为可能使值被修改导致堆性质被破环。
    public:
        std::vector<int> tree;
        Heap(){};
        Heap(std::vector<int>& vec);
        inline int size();
        inline int top();
        inline int get(int node);
        bool isValid(int node);
        void shiftUp(int node);
        void shiftDown(int node);
        void push(int val);
        void pop();
        void remove(int node);
        void set(int node, int val);
    
};

Heap::Heap(std::vector<int>& vec){
    tree =  vec;
    for(int i = size()>>1; i; --i){
        shiftDown(i);
    }
}

inline int Heap::size(){
    return tree.size();
}

inline int Heap::top(){
    if(size() == 0) throw "堆不能为空";
    return get(1);
}

inline int Heap::get(int node){
    if(!isValid(node)) throw "无效节点";
    return tree[node-1];
}

inline int& Heap::_get(int node){
    if(!isValid(node)) throw "无效节点";
    return tree[node-1];
}

bool Heap::isValid(int node){
    return node >= 1 && node <= size();
}

void Heap::shiftUp(int node){ //传入要调整的节点编号
    while(node > 1 && _get(node>>1) < _get(node)){ //如果不是根节点而且父节点小于自己就交换自己和父节点
        std::swap(_get(node>>1), _get(node));
        node >>= 1;
    }
}

void Heap::shiftDown(int node){
    while((node<<1|1) <= size()){ //如果有两个孩子
        int max_chd = _get(node<<1) > _get(node<<1|1) ? node<<1 : node<<1|1; //取较大的孩子
        if(_get(max_chd) > _get(node)){
            std::swap(_get(max_chd), _get(node));
            node = max_chd;
        }
        else break;
    }
    if(node<<1 == size() && _get(node<<1) > _get(node)){ //最后可能出现只有一个子节点的情况，单独判断
        std::swap(_get(node<<1), _get(node));
    }
}

void Heap::push(int val){
    tree.push_back(val);
    shiftUp(size());
}

void Heap::pop(){
    if(size() == 0) throw "堆不能为空";
    if(size() == 1){
        tree.pop_back();
        return;
    }
    std::swap(_get(1), _get(size()));
    tree.pop_back();
    shiftDown(1);
}

void Heap::remove(int node){
    if(size() == 0) throw "堆不能为空";
    while(node > 1){ //向上交换到根节点
        std::swap(_get(node>>1), _get(node));
        node >>= 1;
    }
    pop();
}

void Heap::set(int node, int val){
    if(val > _get(node)){
        _get(node) = val;
        shiftUp(node);
    }
    if(val < _get(node)){
        _get(node) = val;
        shiftDown(node);
    }
}

//以上的代码在简介里的那篇文章中有讲解

void heapSort(int *begin, int *end){
    std::vector vec(begin, end);
    Heap hp(vec);
    for(int *p = begin; p != end; ++p){
        *p = hp.top();
        hp.pop();
    }
}