主定理的应用范例

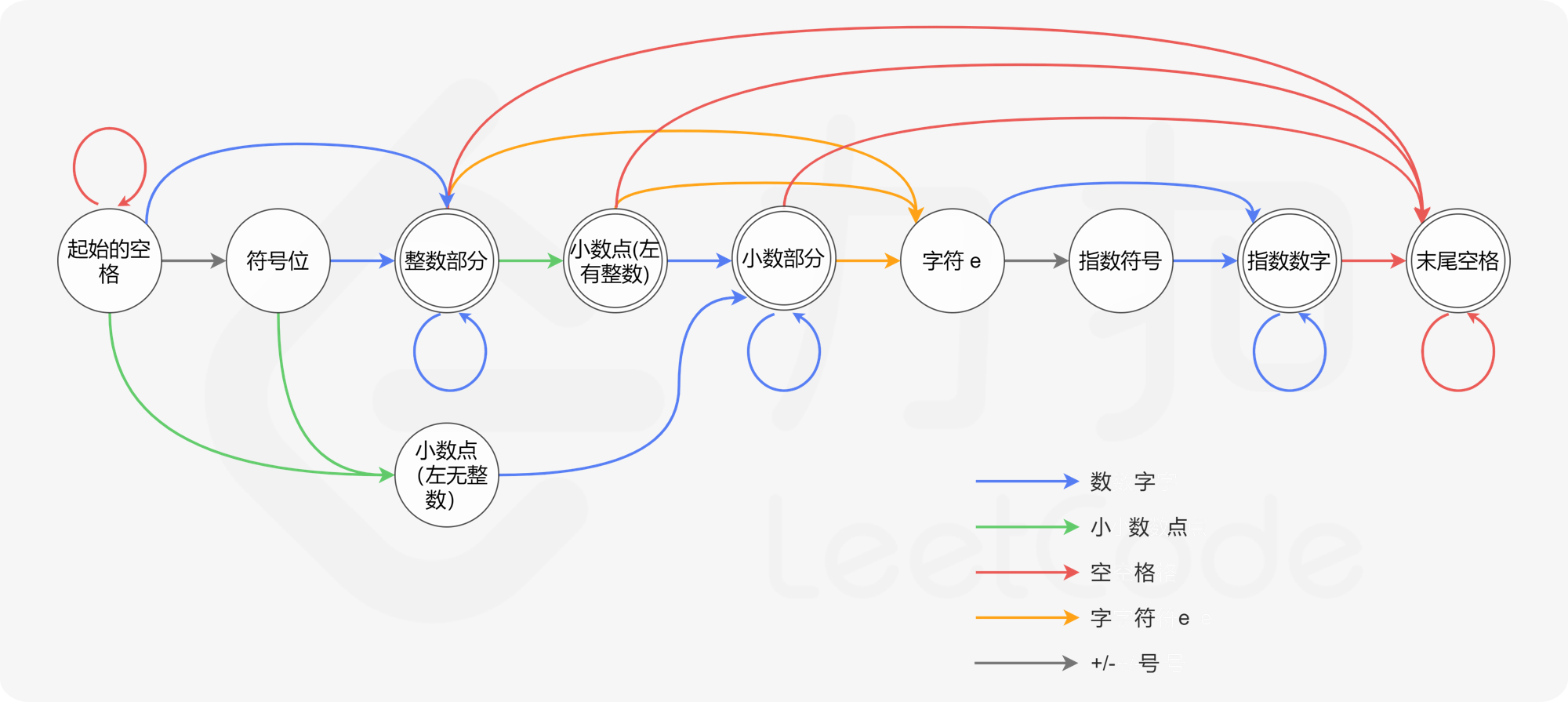
前置知识——渐进复杂度记号

本文假设你已经掌握了渐进复杂度的含义，并且熟悉大O记号表示复杂度。除了大O记号外，这里再简单介绍一下其他的复杂度记号。如果你掌握了这些符号，可以跳过本段。

渐进复杂度的记号有$\Theta$、$O$、$\Omega$、$o$、$\omega$，主定理用到了前三个，但为了完整性这里全部介绍。

$\Theta$

若$\exists c_1,c_2,n_0 \gt 0$，使得$\forall n \geq n_0$有$c_1 \cdot g(n) \leq f(n) \leq c_2 \cdot g(n)$，则称$f(n) = \Theta(g(n))$

$\Theta$可以精确的表示算法的渐进复杂度，相应地，使用时也要注意严谨性。

用表示大小的符号类比的话，$\Theta$就相当于$=$等于号。

$O$

若$\exists c,n_0 \gt 0$，使得$\forall n \geq n_0$有$f(n) \leq c \cdot g(n)$，则称$f(n) = \Theta(g(n))$

虽然大O记号不如$\Theta$记号来的精确，但它是讨论复杂度的时候最常用的符号。主要是因为比较好用键盘输入，并且它指出了我们关心的运行时间上界（尤其是当一些算法的下界不太好计算得出时）

用表示大小的符号类比的话，$O$就相当于$\leq$小于等于号。

$\Omega$

若$\exists c,n_0 \gt 0$，使得$\forall n \geq n_0$有$f(n) \geq c \cdot g(n)$，则称$f(n) = \Omega(g(n))$

用表示大小的符号类比的话，$O$就相当于$\geq$大于等于号。

$o$

若 $\forall c>0,\;\exists n_0>0$，使得 $\forall n \geq n_0$ 有 $f(n)<c\cdot g(n)$，则称$f(n) = o(g(n))$

用表示大小的符号类比的话，$o$就相当于$<$小于号。

$\omega$

若 $\forall c>0,\;\exists n_0>0$，使得 $\forall n \geq n_0$ 有 $f(n)>c\cdot g(n)$，则称$f(n) = \omega(g(n))$

用表示大小的符号类比的话，$\omega$就相当于$>$大于号。

整理

为了便于记忆，可以整理成下面的表格。

复杂度记号	帮助记忆
$\Theta$	$=$
$O$	$\leq$
$\Omega$	$\geq$
$o$	$\lt$
$\omega$	$\gt$

介绍

主定理（Master Theorem）是用于分析分治算法复杂度的常用方法，给定算法运行时间与输入规模的函数的递推关系式，就可以计算得到算法的渐进时间复杂度。

若$T(n) = aT(\frac{n}{b}) + f(n)$其中$a \geq 1, b \gt 1$

其中：

• $n$是问题规模
• $a$是分治的子问题数量
• $\frac{n}{b}$是每个子问题的规模（b>1）
• $f(n)$是分治算法需要的额外时间（即拆分成子问题的用时，以及将子问题的答案合并成最终结果的用时）

有：

$$T(x)=\begin{cases} \Theta(n^{\log _b a}), & \text{if $\exists \varepsilon \gt 0, f(n)=O(n^{\log _b (a) - \varepsilon})$}\\ \Theta(n^{\log _b a}\log ^{\varepsilon + 1} n), & \text{if $\exists \varepsilon \geq 0, f(n)=\Theta(n^{\log _b a}\log ^\varepsilon n)$}\\ \Theta(f(n)), & \text{if $\exists \varepsilon \gt 0, f(n)=\Omega(n^{\log _b (a) + \varepsilon})$}\\ &\text{meanwhile $\exists c \lt 1$, for sufficiently large $n$, $f(\frac{n}{b}) \leq cf(n)$} \end{cases}$$

为了方便理解和记忆，也可以不严谨地写成这样

$$T(x) = \begin{cases} \Theta(n^{\log _b a}), & \text{if $f(n) \lt n^{\log _b a}$}\\ \Theta(f(n) \log n), & \text{if $f(n) = n^{\log _b a} \log ^k n \quad (k \geq 0)$}\\ \Theta(f(n)), & \text{if $f(n) \gt n^{\log _b a}$}\\ \end{cases}$$

注意，这里的$\lt$、$=$、$\gt$并不是字面上的意思，只是为了方便理解记忆。真正的含义请看原式子

也就是说，只要比较$f(n)$和$n^{\log _b a}$的大小（多项式比大小）。哪一个大，$T(n)$就等于$\Theta(\text{哪个})$，如果一样大，或者相差$\log ^k n$，那么T(n)就等于$\Theta(f(n)\log n)$，是不是很简单。

如果只考虑$f(n)=n^d$的情况，那么就更简单了

$$T(x) = \begin{cases} \Theta(n^d \log n), & \text{if $d = \log _b a$}\\ \Theta(n^{\max \{ d, log _b a \}}), & \text{otherwise}\\ \end{cases}$$

实例

这几个例子的复杂度其实不使用主定理也能很容易看出来，这里只是用做例子，方便理解主定理具体是怎么应用的。对于更复杂问题的分治，相对来说就没那么容易看出来了，这时候主定理也就能派上用场了。

二分查找

在二分查找的例子中，$n$表示查找范围的大小，每一次执行二分查找时，查找范围减半，$b=2$，子问题数量仍为1，$a=1$，每一次二分用时是$O(1)$的

$n^{\log _b a} = 1$与f(n)同阶，则$T(n)=\Theta(f(n)\log n)=\Theta(\log n)$

遍历二叉树

$$\begin{align*} a &= 2\\ b &= 2\\ f(n) &= O(1)\\ n^{\log _b a} &= n \end{align*}$$

$n$比$f(n)$大，因此$T(n)=f(n)=\Theta(n)$

归并排序

归并排序中，$a=b=2$，而$f(n)$等于多少呢？我们考察归并的过程，两个已经排序好的数组合并成一个时，比较操作的次数是 $O(n)$ 的，而将元素转移到临时数组再转移回来所用的时间也是$O(n)$的，显然$f(n)=O(n)$

$n^{\log _b a} = n$与$f(n)$同阶，则$T(n)=n \log n$