半加器、全加器与超前进位加法器

半加器(Half Adder)

半加器接受两个输入A、B，输出加法的计算结果S和进位C，表达式及真值表如下：

$$\begin{align*} S &= A \oplus B \\ C &= AB \end{align*}$$

A	B		S	C
0	0		0	0
0	1		1	1
1	0		1	1
1	1		0	1

利用异或门可以很简单的设计出一个半加器

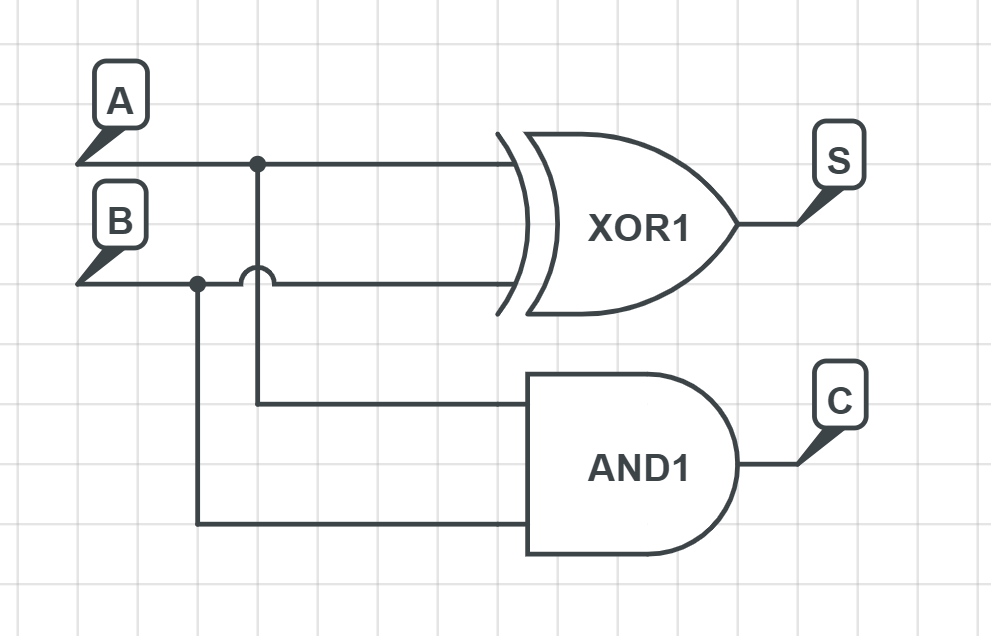
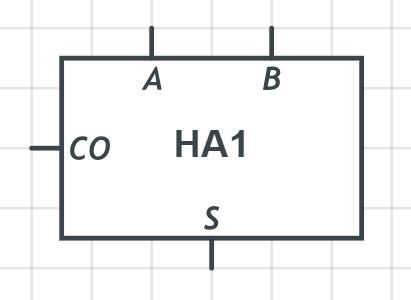
我们把它抽象成这样

全加器(Full Adder)

如果我们需要将低位所位的1也加上，就需要用到全加器，它接受三个输入A、B和C，输出加法的计算结果S和进位C1。由此可以写出全加器的表达式。

$$\begin{align*} S &= A \oplus B \oplus C \\ C_1 &= AB + AC + BC \end{align*}$$

*这里的乘法和加法分别代表布尔代数中的“与”和“或”，而“$\oplus$”是异或

第一个式子很好理解，因为逻辑门里面的异或就是不进位的加法。而第二个式子翻译成人话就是“A、B、C中至少有两个为真”，也就是有进位的情况。

根据表达式可以列出它的真值表。

A	B	C		S	C1
0	0	0		0	0
0	0	1		1	0
0	1	0		1	0
0	1	1		0	1
1	0	0		1	0
1	0	1		0	1
1	1	0		0	1
1	1	1		1	1

具体的实现也很简单，只需要用到两个半加器。

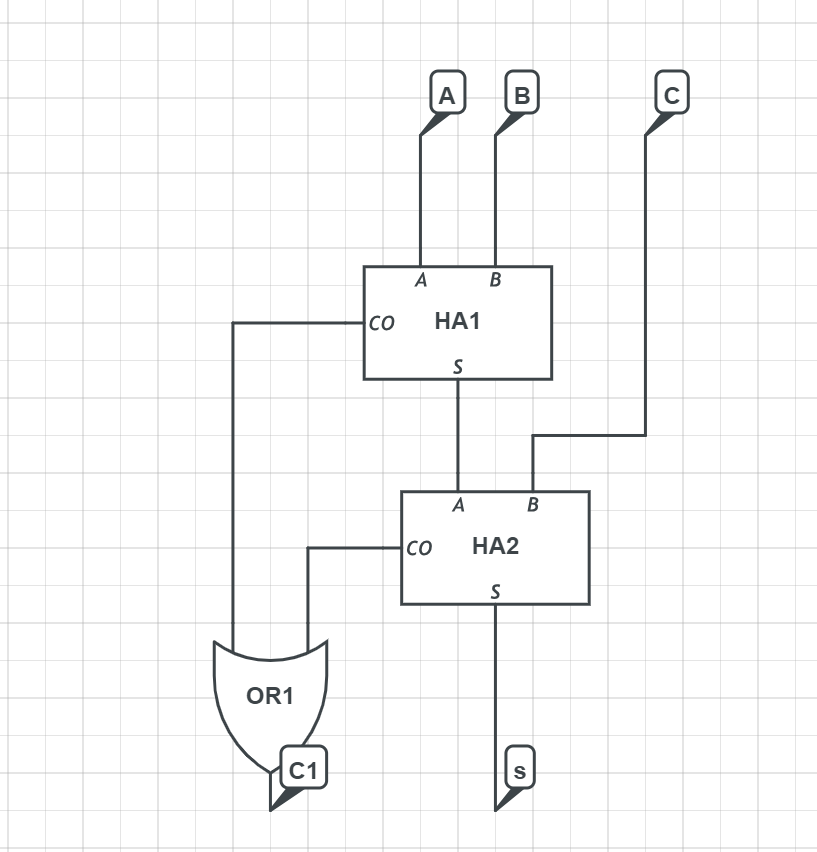
同理我们把它抽象（或者说封装）成这样：

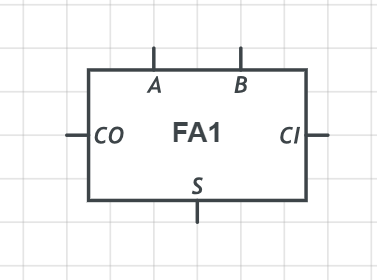
有了全加器和半加器，制作一个n位加法器就很简单了，这里以4位加法器为例。

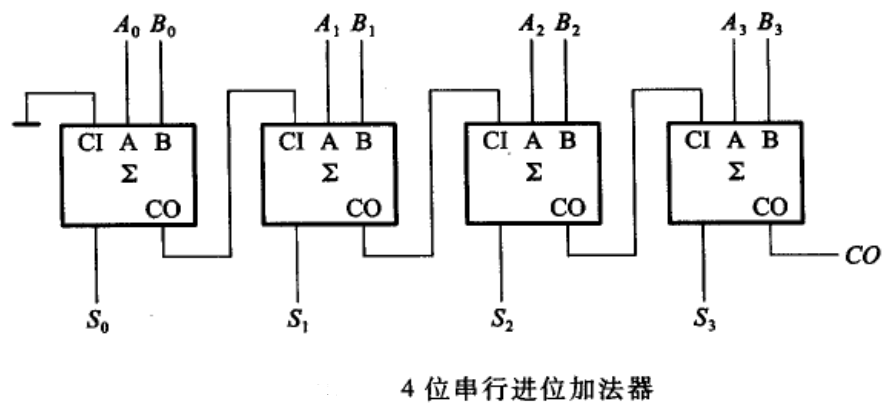
这种加法器被称为串行进位加法器(Ripple Carry Adder, RCA)，也叫行波进位加法器或脉冲进位加法器，RCA的特点是电路简单，但由于高位必须等到低位运算完成才能进行，电路产生的延时很大，运算速度较慢，而且位数越多运算越慢。而超前进位加法器(Carry Look-ahead Adder, CLA)可以解决这个问题。

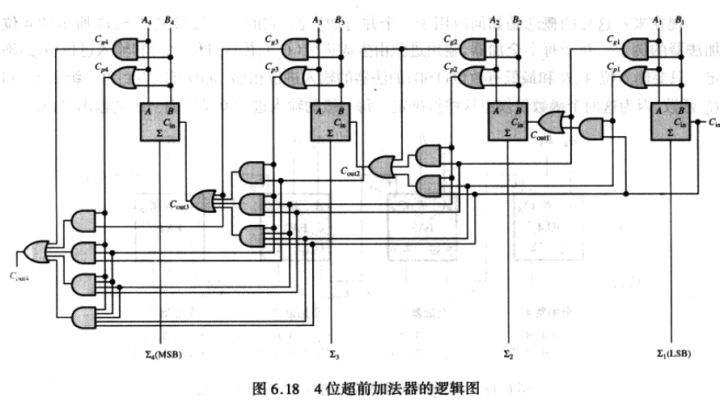
超前进位加法器

上面全加器的式子还有另一种写法

$$\begin{align*} C_{i+1} &= A_i B_i + A_i C_i + B_i C_i\\ &= A_i B_i + (A_i + B_i)C_i\\ S_i &= A_i \oplus B_i \oplus C_i \\ &= (A_i + B_i) \oplus (A_i B_i) \oplus C_i \end{align*}$$

由此，不妨令

$$\begin{align*} G_i &= A_i B_i\\ P_i &= A_i + B_i \end{align*}$$

则有

$$\begin{align*} C_{i+1} &= G_i + P_i C_i\\ S_i &= P_i \oplus G_i \oplus C_i \end{align*}$$

利用这个我们可以提前计算出进位，降低计算的延迟。

$$\begin{align*} C_1 &= G_0 + P_0 C_0\\ C_2 &= G_1 + P_1(G_0 + P_0 C_0)\\ &= G_1 + P_1 G_0 + P_1 P_0 C_0\\ C_3 &= G_2 + P_2(G_1 + P_1 G_0 + P_1 P_0 C_0)\\ &= G_2 + P_2 G_1 + P_2 P_1 G_0 + P_2 P_1 P_0 C_0\\ &\ldots \ldots \end{align*}$$

进位延时只有三个门的延时，加上最后一级全加器的延时，最多四个延时时间。
具体的实现比较复杂，如图。