引入

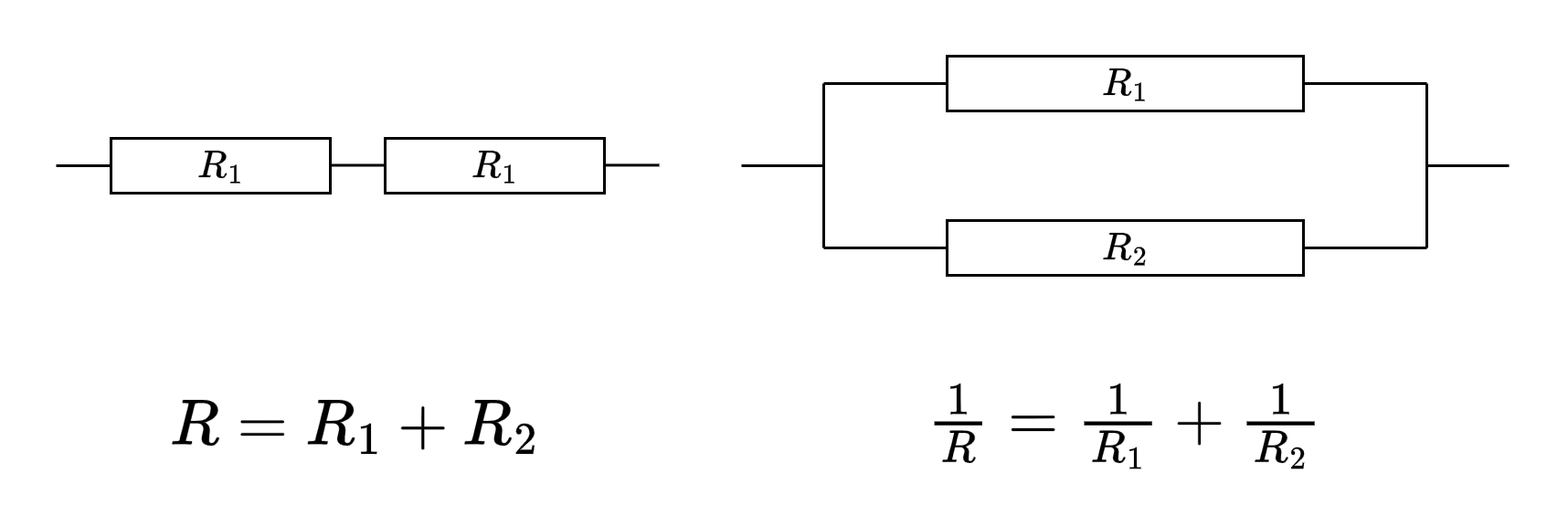
我们早就学过了计算串并联电阻的等效电阻的公式：

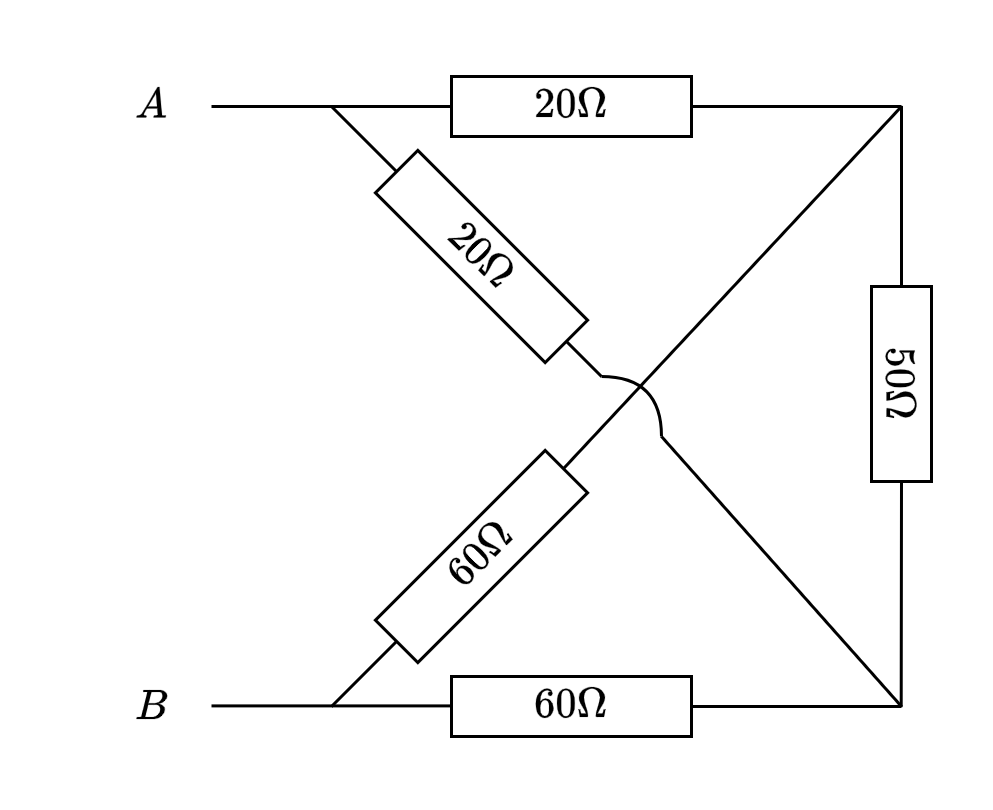
针对混合的电阻网络，有些时候我们依然可以反复运用这两个公式来计算等效电阻。在有些电阻网络中，这样是无法得到答案的：

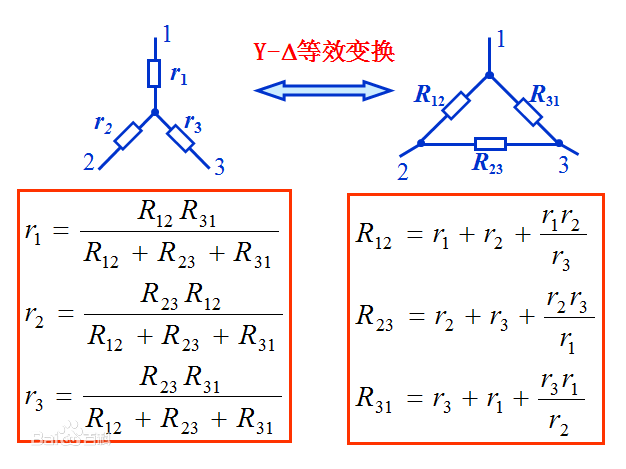
如果你熟悉星三角变换，你应该能很快算出答案。（或者你能看出这就是一个平衡桥，那就能口算了）

星三角变换固然是一种手工计算等效电阻的很好方法，但是对于计算机而言，利用这个方法计算电阻会很麻烦。下面，我将使用高斯消元法来计算两点之间的等效电阻。

建模

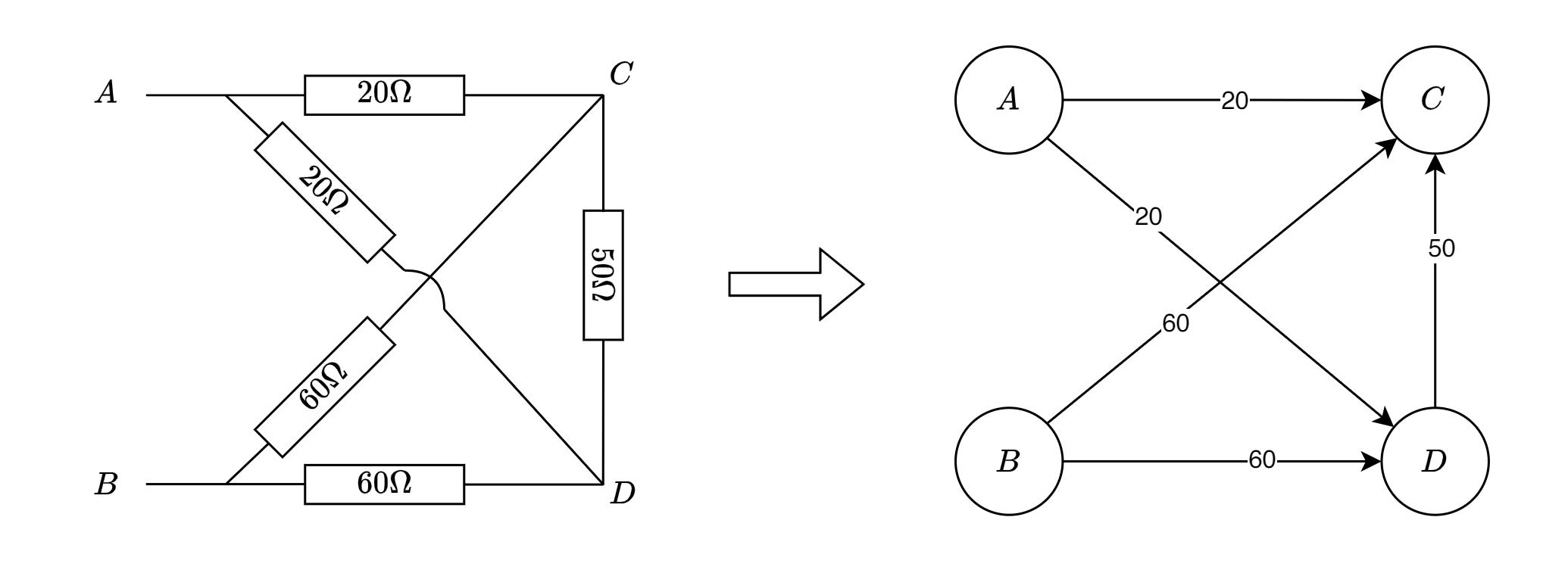
我们可以把两点之间的纯电阻网络看作是一张有向图，节点表示导线，边表示电阻，边权表示电阻的大小。要求源点和汇点之间的等效电阻大小。

为什么要建成有向边呢，因为虽然电阻是无向的，但是电流是有向的，我们一开始并不知道电流的方向，但是可以任意地假定一个方向，然后给每一条边赋上一个电流IiI_i，当IiI_i为正，表示电流方向与箭头同向，当IiI_i为负，表示电流方向与箭头反向。然后我们再假定汇点的电势为00，其余每个节点赋上一个电势φi\varphi_i。

若要求源点到汇点的等效电阻，只需要知道源点的电势φs\varphi_s和汇点的电势φt\varphi_t，以及汇入汇点的总电流II，就可以计算出等效电阻R=φs−φtIR = \frac{\varphi_s - \varphi_t}{I}。为了计算这些量，我们要把整个网络的电流和电势都算出来。

设这张图共有nn节点mm条边，则我们一共有mm个IiI_i未知，n−2n-2个φi\varphi_i未知。一共m+n−2m+n-2个未知量，需要m+n−2m+n-2个方程才能解出来。我们可以利用所学的物理知识来找到这些方程。

欧姆定律

最简单的就是安培定律了，对于编号为ii的边(u,v)(u, v)，有

φu−φv=IiRi\begin{align*} \varphi_u - \varphi_v = I_i R_i\\ \end{align*}

这一共有mm个方程。

基尔霍夫电流定律（KCL）

除了源点和汇点外，每个结点流入的电流都等于流出的电流。

对于编号为uu的节点，有

∑i∈Adj(u)Ii=0\sum_{i \in Adj(u)} I_i = 0

这 n−2n-2 个方程，再加上前面的 mm 个，正好有 m+n−2m+n-2 个方程，我们可以用高斯消元法来解出所有的电流。

高斯消元法

现在不妨令 φs=1\varphi_s = 1，φt=0\varphi_t = 0，则有

{φu−φv=IiRi∀(u,v)∈E∑i∈Adj(u)±Ii=0∀u∈V−{s,t}φs=1φt=0\begin{cases} \varphi_u - \varphi_v = I_i R_i && \forall (u, v) \in E \\ \sum_{i \in Adj(u)} \pm I_i = 0 && \forall u \in V - \{s, t\} \\ \varphi_s = 1 \\ \varphi_t = 0 \\ \end{cases}

有了这 m+nm+n 个方程，我们就可以用高斯消元法解出所有的电势和电流，进而求出等效电阻了。

高斯消元法是一种求解线性方程组的算法，在计算机中的实现也很简单。此处复杂度O((m+n)3)O((m+n)^3)

此处的优化空间：从上面可以看出，这些方程一般是很稀疏的，如果改用计算稀疏线性方程组的算法可以达到更高的效率。如LU分解、bfgs、lbfgs

代码实现

使用纯C实现

Github地址：https://github.com/cyrus28214/resistance

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
#include <stdio.h>
#include <stdlib.h>
#include <math.h>

double **array2d(int rows, int cols);
void gauss(double **a, int n);

int main() {
    int n, //节点数量
        m, //边的数量
        s, //源点
        t; //汇点
    //图不能有自环，可以有重边，需要联通

    scanf("%d%d%d%d", &n, &m, &s, &t);

    //为了代码方便，增加一个变量I_总
    int k = n + m + 1; //方程的个数

    double **a = array2d(k, k+1);//多出的一列是等号右边的常数
    //每一列代表的变量分别为：
    // I_0 ... I_{m-1} | phi_0 ... phi_{n-1} | I_总
    //I_i = a[][i]
    //phi_i = a[][m+i]

    //各个方程为
    //0 ~ m-1 欧姆定律： phi_u - phi_v - I_i R_i = 0
    //m ~ m+n-1 KCL:    sum I_i = 0 (对非源点汇点)
    //                  phi_s = 1 (对源点，加1V电压)
    //                  phi_t = 0 (对汇点，接地)
    //m+n：             计算总电流I_总=汇入t电流

    //m行，每行三个整数u, v, r表示u到v有一个阻值为r的电阻
    for (int i = 0; i < m; i++) {
        int u, v;
        double r;
        scanf("%d%d%lf", &u, &v, &r);

        //欧姆定律
        a[i][m+u] = 1;
        a[i][m+v] = -1;
        a[i][i] = -r;
        //第i个方程 phi_u - phim+n- I_i R_i = 0

        //KCL 注意电流方向，这里按流出为负，流入为正
        if (u != s && u != t) a[m+u][i] = -1;
        else if (u == t) a[m+n][i] = -1;
        if (v != s && v != t) a[m+v][i] = 1;
        else if (v == t) a[m+n][i] = 1;
    }

    a[m+s][m+s] = 1, a[m+s][k] = 1; //源点电电势为1V
    a[m+t][m+t] = 1, a[m+t][k] = 0; //汇点电势为0
    a[m+n][m+n] = -1; //计算总电流I_总

    gauss(a, k); //求解方程组

    double I_total = a[k-1][k];
    printf("%6e\n", 1 / I_total);//由于我们设定了整体电压为1，最后的等效电阻就是1/I_总
}

//生成一个rows行cols列的二维数组，全部初始化成0
double **array2d(int rows, int cols) {
    double **arr = malloc(rows * sizeof(double *));
    for (int i = 0; i < rows; i++) {
        arr[i] = calloc(cols, sizeof(double));
    }
    return arr;
}

void gauss(double **a, int n) {
    //高斯-约旦消元法求解线性方程组
    for (int i = 0; i < n; i++) { //当前行
        //将当前行替换为列主元最大的行
        for (int j = i + 1; j < n; j++) {
            if (fabs(a[j][i]) > fabs(a[i][i])) {
                double *temp = a[i];
                a[i] = a[j];
                a[j] = temp;
            }
        }

        double c = a[i][i];
        //通常的算法此处需要特判c是否为0，但根据物理意义，本问题一定有唯一解，可以不用。
        for (int k = 0; k <= n; k++) 
            a[i][k] /= c;

        //消元
        for (int j = 0; j < n; j++) {
            if (i == j) continue;
            c = a[j][i];
            for (int k = 0; k <= n; k++)
                a[j][k] -= c * a[i][k];
        }
    }
}

验证

对于开头的这个例子，我们可以验证一下：

输入

1
2
3
4
5
6
7
4 5 0 1
0 2 20
0 3 20
1 2 60
1 3 60
3 2 50
4.000000e+01

输出4.000000e+01，和手算结果一致

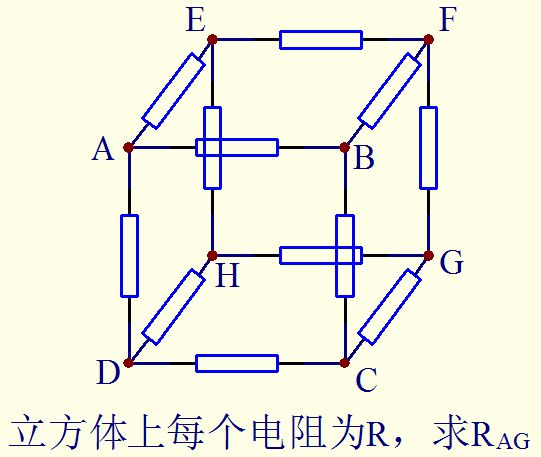
再来一个例子，经典高中物理题，每个电阻都是1Ω1\Omega，求对角线电阻：

用我们的程序算出：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
8 12 0 6
0 1 1
1 2 1
2 3 1
3 0 1
4 5 1
5 6 1
6 7 1
7 4 1
0 4 1
1 5 1
2 6 1
3 7 1
8.333333e-01

而这一题的答案是5/6 Ω5 / 6 \,\Omega，答案正确。

一些私货

qzqz机房的hxd们可以在cofun上看到我出的这一题，快去做（cofun服务器好像又爆炸了）

如果你不知道cofun是什么，请忽略这段私货。