Diffie–Hellman密钥交换以及OpenSSL中相关源码解析
什么是 Diffie–Hellman 密钥交换?
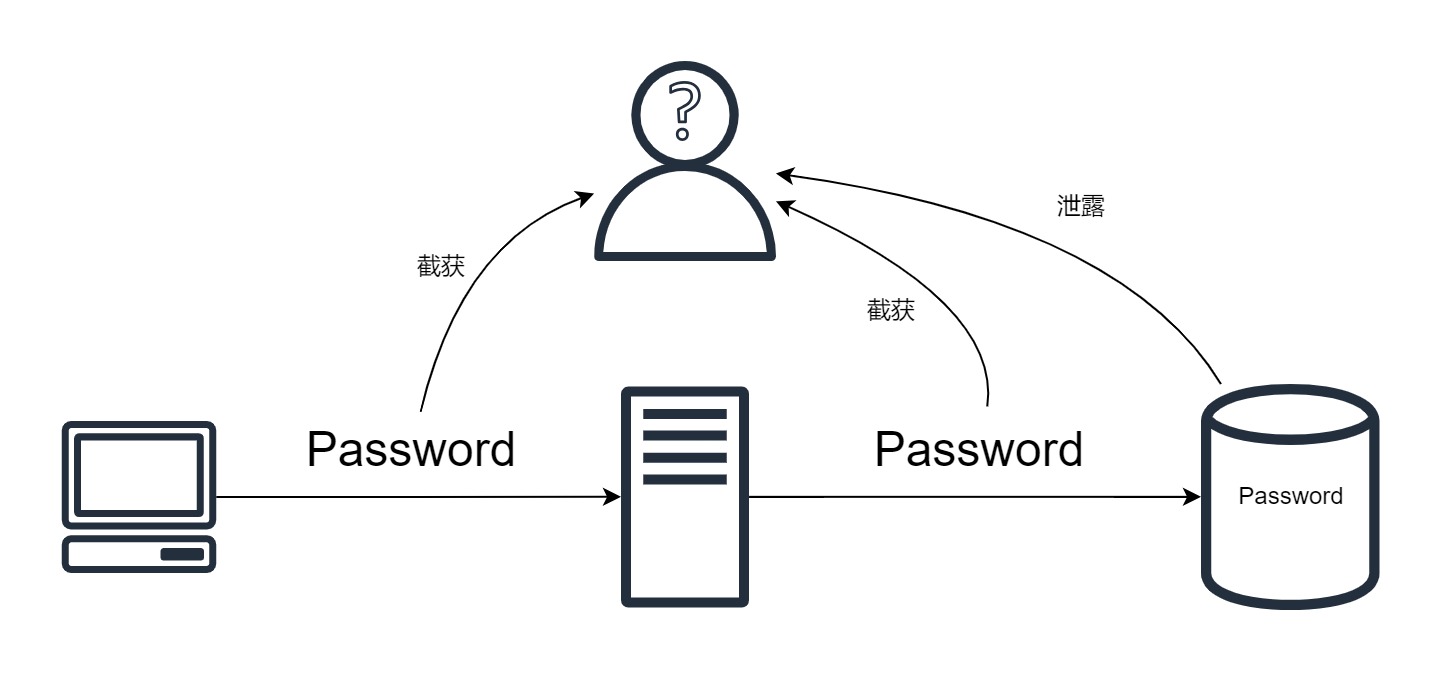
Diffie-Hellman是一种密钥交换方法,可以让双方从不安全信道中建立一个共同的密钥来加密通讯内容。
DH方法本身很简单,但它却是许多现代安全协议的基础,如TLS安全传输层协议,安全外壳协议以及IPSec互联网安全协议,都部分使用到了DH算法。
Diffie–Hellman 密钥交换的过程
Diffie-Hellman密钥交换的过程如下:
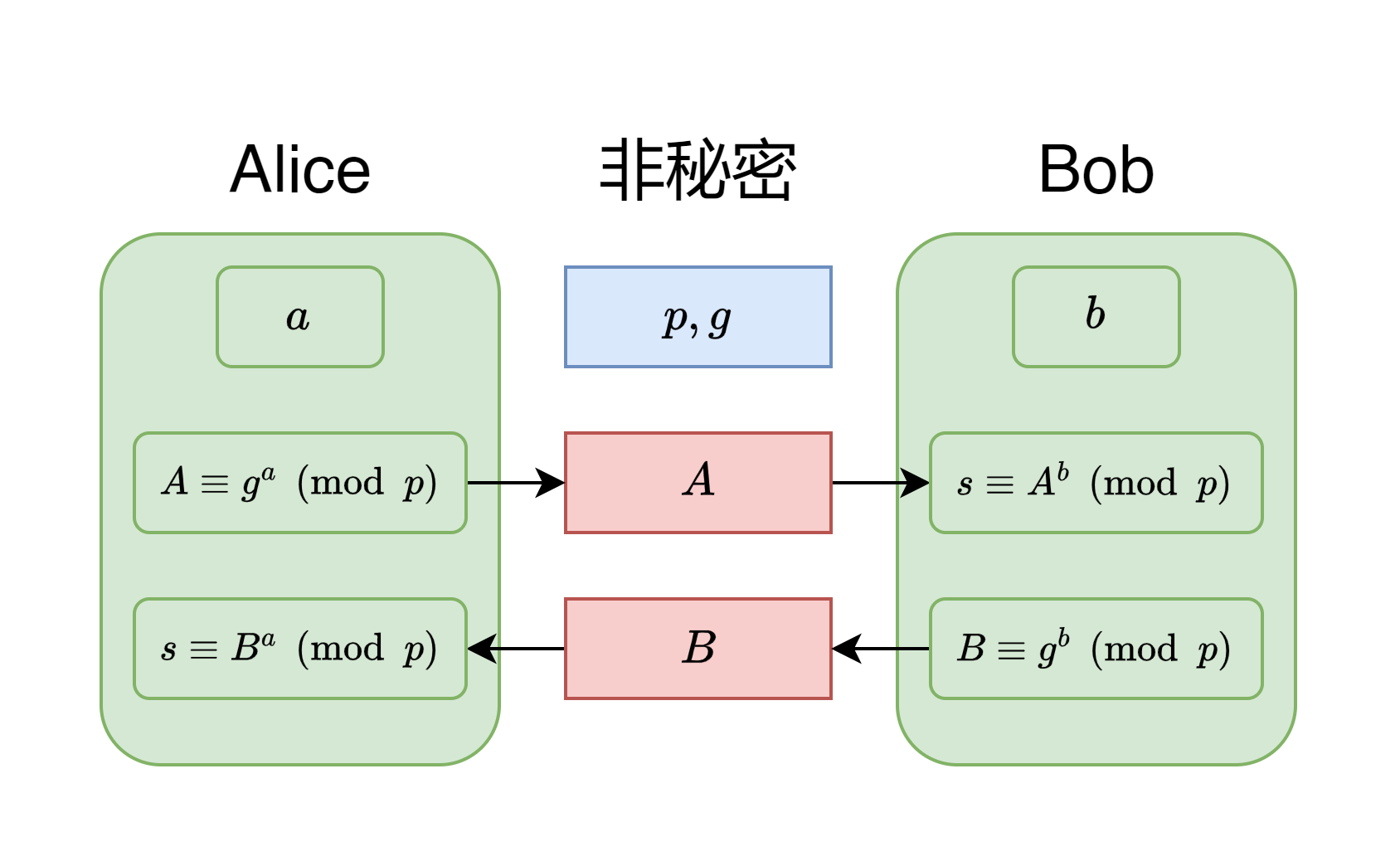
- 双方协定一个质数和基数。这两个数无需保密,可以随意协商或传输。
- Alice生成一个随机数,并计算 。
- Bob生成一个随机数,并计算。
- Alice发送给Bob。
- Bob发送给Alice。
- Alice计算
- Bob计算
由于 ,双方计算出来的是同一个数,双方成功交换了一个共享密钥。后续的通信可以基于进行。
不难发现,窃听的第三方只知道和,无法计算出。
与RSA不同,生成DH密钥的速度非常快。因为RSA要求公钥和私钥都是大质数,而DH没有这个限制。
安全性
中间人攻击
DH只是一种密钥交换方法。并没有身份验证的功能。DH无法抵御中间人攻击,中间人有办法向Alice伪装成Bob,向Bob伪装成Alice。要解决这个问题,必须引入一个认证机构(Certificate Authority, CA)。这就是一个老生常谈的问题了。
完美前向保密性(Perfect Forward Secrecy)
首先要注意的是,在英语语境中,前向(forward)指的是“向过去”,而后向(backward)指的是“向未来”。我经常记反。例如“向前兼容(forward compatibility)”指的是兼容过去的版本,而“向后兼容(backward compatibility)”指的是兼容未来的版本。
这里,完美前向保密性(PFS)指的是,即使密钥泄露,之前的对话内容也无法被破解。
DH方法可以保证前向安全性。假如攻击者记录了历史的所有对话,并盗取一方的私钥,也无法恢复出历史对话。因为每一次DH使用的参数都是临时的,会在密钥交换结束后销毁。(使用固定参数的DH不是PFS的)
离散对数
就像RSA算法的安全性依赖于大素数分解的难度一样。Diffie-Hellman密钥交换的安全性依赖于离散对数的计算难度。随着量子计算的发展,如果出现了高效的解决离散对数的算法,那么DH和基于DH的加密方法都将变得不安全。
目前,有一些DH方法的变种旨在解决后量子密码学挑战下的密钥交换,如Post-Quantum Extended Diffie-Hellman(PQXDH)
在其他群上的扩展
原始的DH算法定义在整数乘法群上,事实上,可以改变这个群给出DH的不同变种。
例如,DH方法有一种变种叫做Elliptic Curve Diffie-Hellman(ECDH)。ECDH使用椭圆曲线的乘法来代替质数阶模乘法,提供了更高的安全性。在同等的安全级别下,ECDH只需要更短的密钥,使ECDH的计算效率也得到提升。
OpenSSL中的Diffie–Hellman实现
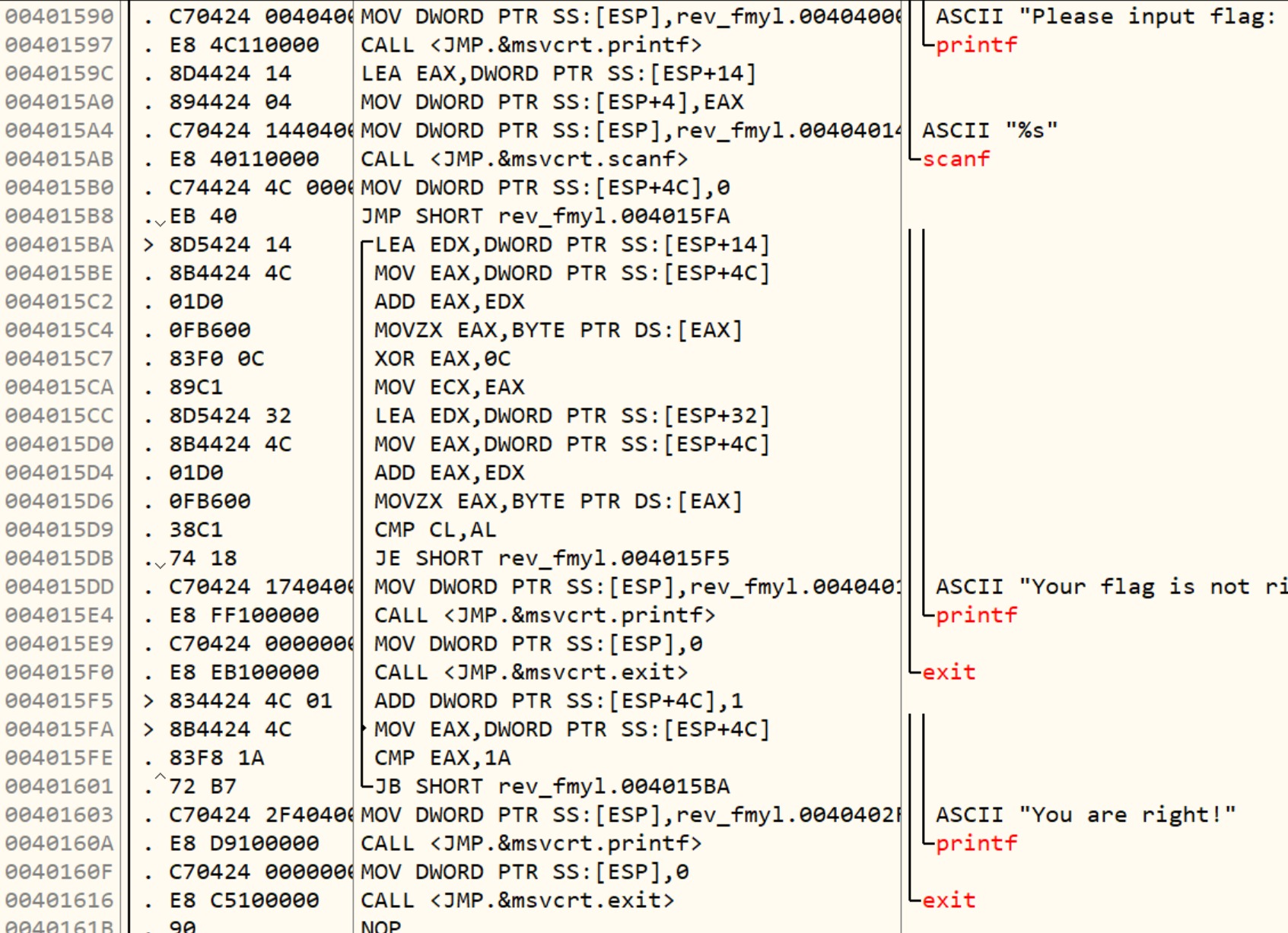
OpenSSL中实现了Diffie–Hellman算法,相关代码如下:
1 | int ossl_dh_compute_key(unsigned char *key, const BIGNUM *pub_key, DH *dh) |
DH算法的实现非常简单,上面这段代码的核心部分只有4.和5.两处。尤其需要注意5.的部分,假如Z = 1或Z = p-1,这两个数是模p乘法群中的平凡元素,很容易作为加密系统的弱点被攻击。
参考链接
https://en.wikipedia.org/wiki/Diffie%E2%80%93Hellman_key_exchange
https://en.wikipedia.org/wiki/Elliptic-curve_Diffie%E2%80%93Hellman
https://www.techtarget.com/searchsecurity/definition/Diffie-Hellman-key-exchange
https://stackoverflow.com/questions/14034508/dh-vs-dhe-and-ecdhe-and-perfect-forward-secrecy
https://www.geeksforgeeks.org/difference-between-diffie-hellman-and-rsa/