实现常用排序算法(三)堆排序
简介
堆排序就是利用堆进行排序,如果对堆这种数据结构不熟悉可以看一看我的这篇文章。
堆排的思想很简单,就是在需要排序的数组上建立堆,然后执行pop操作,直到堆为空,因为每次pop出来的元素都是堆中的最大/最小值,所以可以保证出来的元素有序。堆排也是一种不稳定排序,时间复杂度O(nlogn)O(n \log n)O(nlogn)。堆排序相比于先前两种排序的优势是它不需要递归,堆排序使用了更少的栈空间,防止因递归层数过多引发的低效(尤其是对于快排来说)。
实现
只要实现了堆的代码,堆排就很简单了。
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117class ...
主定理的应用范例
前置知识——渐进复杂度记号
本文假设你已经掌握了渐进复杂度的含义,并且熟悉大O记号表示复杂度。除了大O记号外,这里再简单介绍一下其他的复杂度记号。如果你掌握了这些符号,可以跳过本段。
渐进复杂度的记号有Θ\ThetaΘ、OOO、Ω\OmegaΩ、ooo、ω\omegaω,主定理用到了前三个,但为了完整性这里全部介绍。
Θ\ThetaΘ
若∃c1,c2,n0>0\exists c_1,c_2,n_0 \gt 0∃c1,c2,n0>0,使得∀n≥n0\forall n \geq n_0∀n≥n0有c1⋅g(n)≤f(n)≤c2⋅g(n)c_1 \cdot g(n) \leq f(n) \leq c_2 \cdot g(n)c1⋅g(n)≤f(n)≤c2⋅g(n),则称f(n)=Θ(g(n))f(n) = \Theta(g(n))f(n)=Θ(g(n))
Θ\ThetaΘ可以精确的表示算法的渐进复杂度,相应地,使用时也要注意严谨性。
用表示大小的符号类比的话,Θ\ThetaΘ就相当于===等于号。
OOO
若∃c,n0>0\exists c,n_0 \gt 0 ...
图解基础数据结构——堆
前言
原本打算写“实现常用排序算法(三)堆排序”,结果用了太多的篇幅讲解堆,于是单独出来写成专门讲解堆的博客,后面在简短的写一写堆排序的实现。
简介
堆其实是很基础的数据结构,堆往往是初学者学习的第一个树形数据结构,排在数组、链表、队列、栈等线形数据结构之后。但其实堆并没有那么好理解,而且也常常被忽略(特别是对于OIer来说),因为经常可以直接调包使用,不需要手写堆,C++内置了std::priority_queue,python也有import heapq。
堆的思想简洁明了——大的在上面;堆的实现高效优雅——只需要维护一个数组;堆的插入、删除、修改的时间复杂度都是一样的 O(logn)O(\log n)O(logn) ,因此堆绝对值得好好地理解并且手写一个出来。
一般来说,只要满足父节点的值比子节点大就可以称作堆,但是在具体实现上,最常用的还是二叉堆,也就是同时满足堆性质和二叉树性质的堆,除了二叉堆以外,还有二项堆、斐波那契堆等。通常说的堆指的都是二叉堆。
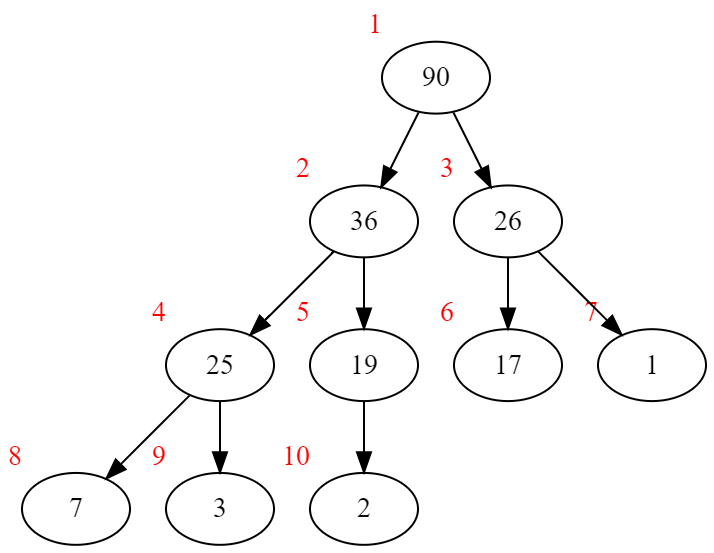
堆的储存
注意:以下默认为最大堆(Max Heap),最小堆(Min Heap)也是同理
要储存堆,首先要给堆中的每个结点 ...
实现常用排序算法(二)归并排序
简介
归并排序排序(Merge Sort)与快速排序不同,它是一种稳定排序(Stable Sort),也就是说,对于数组中相等的元素,归并排序可以保证它们排序后相对位置不改变。由于我们用整数int的数组的排序作例子,这个特点并不能很好地表现出来,实际上在某些场景中这个性质很重要,因此c++特别地在std::sort之外提供了一个稳定排序算法std::stable_sort。
归并排序也是分治算法,归并排序重复进行合并操作,不断地将两个排序好的数组合并成一个排序好的数组,最终完成整个数组的排序。归并排序有两种实现,一种是空间复杂度O(1)O(1)O(1)的原地(In-place)算法,另一种需要额外O(n)O(n)O(n)的空间。
不使用额外空间的归并排序需要用到一个叫做手摇算法(Block Swap Algorithm/内存反转算法/三重反转算法)的技巧来交换数组中的两块内存,这会引入大量的变量交换操作从而增加算法消耗的时间,甚至有可能使归并排序退化到O(n2)O(n^2)O(n2),本质上是一种时间换空间的方法,这里不多做介绍。较为常用的还是非原地的常规写法,这里也用这种实现方法来演 ...
实现常用排序算法(一)快速排序
今天来徒手造轮子了,这次是快排!
简介
快速排序(Quick Sort)是非常常用的排序算法,平均时间复杂度为O(nlogn)O(n \log n)O(nlogn),最坏复杂度O(n2)O(n^2)O(n2),是一种不稳定排序。虽然有O(n2)O(n^2)O(n2)的最坏复杂度,但是快排在实践中的效率通常优于其他算法,这也是c++中的std::sort主要使用快排进行排序的原因(std::sort是混合排序算法,并非单一的快排,有空会出一篇文章解析一下其源码)
快排是典型的分治算法,快排选取一个基准值将数组按大小分成两份,一份大于基准值,一份小于基准值,然后对这两份分别递归地进行排序。
在具体实现中,通常用双指针完成这个划分操作,维护两个指针i、j,1到i-1储存≤\leq≤pivot的数,j+1到n储存≥\geq≥pivot的数,然后让i往前,j往后,如果i、j指向的两个元素都不符合条件只需要让两个元素交换就行了,一直移动i、j指针直到两个指针相遇,即完成了划分,然后再递归地进行。
实现
12345678910111213141516void quickSort(int *beg ...
什么时候可以使用滚动数组优化?
Floyd
求全源最短路最常用的就是Floyd算法,代码十分简单,仅需三个for循环。
1234for(k = 1; k <= n; k++) for(i = 1; i <= n; i++) for(j = 1; j <= n; j++) f[i][j] = min(f[i][j], f[i][k] + f[k][j]);
但是,Floyd算法为什么能这么写。为什么枚举k就能算出两点间的最短路?
其实,这段代码是经过所谓滚动数组优化的版本,它原本应该是这样的。
1234for (k = 1; k <= n; k++) for (i = 1; i <= n; i++) for (j = 1; j <= n; j++) f[k][i][j] = min(f[k-1][i][j], f[k-1][i][k] + f[k-1][k][j]);
f[k][i][j]表示只经过编号小于k的节点,从i到j的最短路。
这显然是一个动态规划问题
初始状态:
f[0][i][j] = inf (i != j)
f[0][i][i] ...
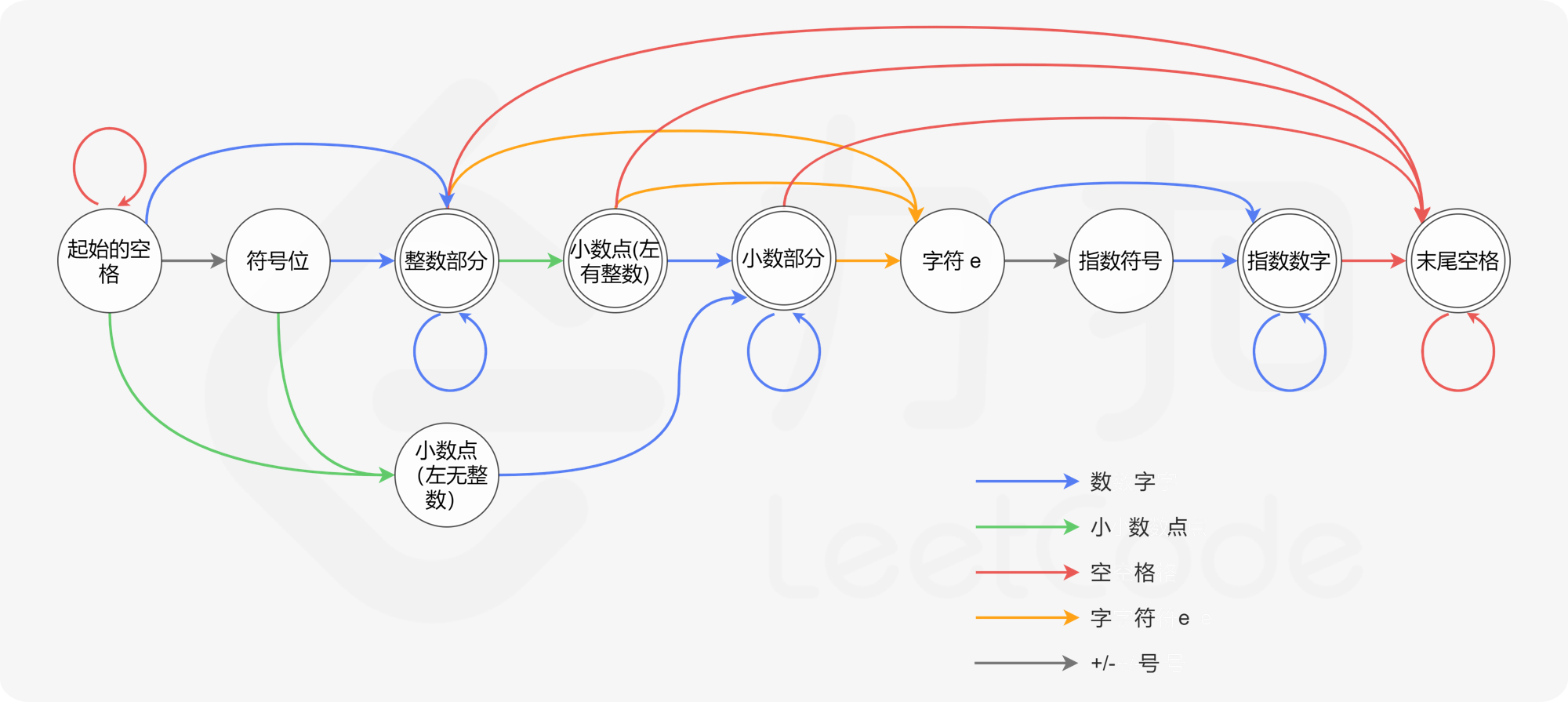
剑指 Offer 20. 表示数值的字符串 题解
题面
请实现一个函数用来判断字符串是否表示数值(包括整数和小数)。
数值(按顺序)可以分成以下几个部分:
若干空格
一个 小数 或者 整数
(可选)一个 'e' 或 'E' ,后面跟着一个 整数
若干空格
小数(按顺序)可以分成以下几个部分:
(可选)一个符号字符('+' 或 '-')
下述格式之一:
至少一位数字,后面跟着一个点 '.'
至少一位数字,后面跟着一个点 '.' ,后面再跟着至少一位数字
一个点 '.' ,后面跟着至少一位数字
整数(按顺序)可以分成以下几个部分:
(可选)一个符号字符('+' 或 '-')
至少一位数字
部分数值列举如下:
["+100", "5e2", "-123", "3.1416", "-1E-16", "0123"]
部分非数值列举如下:
["12e", "1a3.14", "1.2.3", "+-5", " ...
编译的四个步骤:预编译、编译、汇编、链接
假设我们有以下文件:
main.cpp
123456#include<iostream>int main(){ std::cout << "Hello, world!" << std::endl; return 0;}
当我们执行一条命令g++ main.cpp -o main时,实际上g++共完成了四个步骤:
1. 预处理(Preprocessing)
g++ -E main.cpp -o main.i
或许你会注意到,C++程序中有很多以#开头的行,例如#include、#define、#undef、#ifdef等。它们明显与我们通常写的语句不同,如它们无需以分号结尾,它们不可以直接折行。这些被称作预处理指令(Preprocessor Directive)。预处理指令就是在预处理这一步生效的。预处理具体做的工作包括引入头文件、宏的展开、注释的删除等。
2. 编译(Compiling)
g++ -S main.i -o main.s
编译阶段将C/C++代码翻译成汇编指令,这是编译器所做的最核心 ...
C++11方便又常用的特性
不会吧,C++20都出了,不会还有人在学C++11的新特性吧(就是我)。这篇文章介绍一些C++11的方便的语法糖/特性。
auto类型推导
这可以说是C++11中最方便最常用的特性了,一旦开始用就再也回不去了。
1234float foo();auto a = 3; //a的类型是intauto b = foo(); //b的类型是floatauto c; //报错,因为编译器无法推断出c的类型
这个特性在遍历stl容器的时候很好用,例:
1234567891011std::vector<int> array;//传统的方法很长很麻烦for(std::vector<int>::iterator it = array.begin(); it != array.end(); ++it){ //do something}//现在只需这样for(auto it = array.begin(); it != array.end(); ++it){ //do something}
要注意auto可以用于函数返回值但不能用 ...
半加器、全加器与超前进位加法器
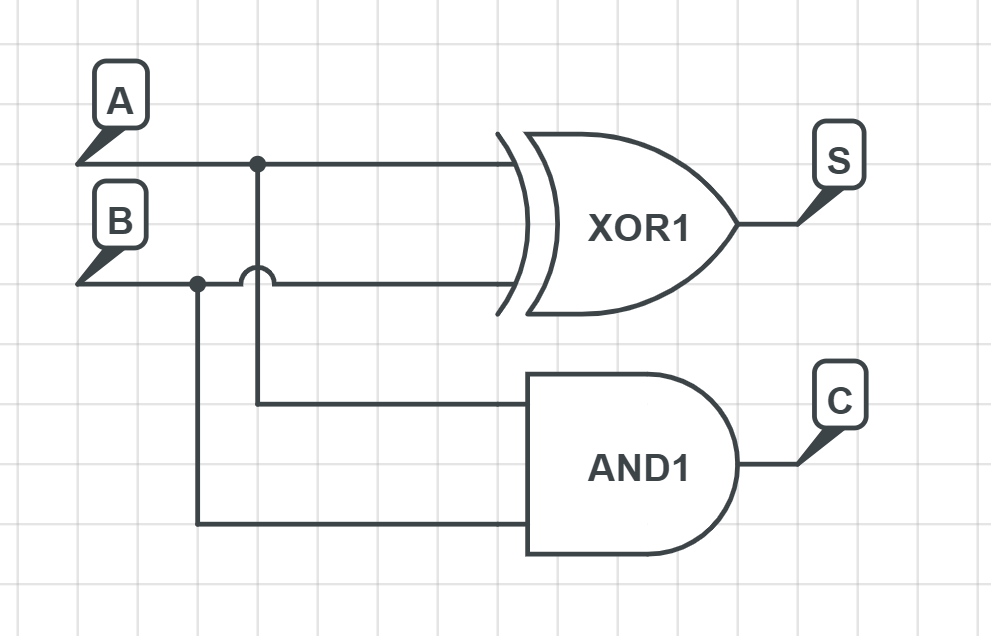
半加器(Half Adder)
半加器接受两个输入A、B,输出加法的计算结果S和进位C,表达式及真值表如下:
S=A⊕BC=AB\begin{align*}
S &= A \oplus B \\
C &= AB
\end{align*}SC=A⊕B=AB
A
B
S
C
0
0
0
0
0
1
1
1
1
0
1
1
1
1
0
1
利用异或门可以很简单的设计出一个半加器
我们把它抽象成这样
全加器(Full Adder)
如果我们需要将低位所位的1也加上,就需要用到全加器,它接受三个输入A、B和C,输出加法的计算结果S和进位C1。由此可以写出全加器的表达式。
S=A⊕B⊕CC1=AB+AC+BC\begin{align*}
S &= A \oplus B \oplus C \\
C_1 &= AB + AC + BC
\end{align*}SC1=A⊕B⊕C=AB+AC+BC
*这里的乘法和加法分别代表布尔代数中的“与”和“或”,而“⊕\oplus⊕”是异或
第一个式子很好理解,因为逻辑门里面 ...