Cyrus' Blog

预赛 签到-签到题 12345678910111213141516171819202122232425262728296L<Ak3,*@VM*>7U&FZFNWc,Ib=t,X!+,BnSDfoaNhdiO*][5F];eV^]Lm&?$'<oeGH&6tqcgK_JDp-3;8wh?Si,G$BarTFjE?b$eR/,Igij<({u90M$5If589[<4+jp%3_%R(526#1J|m5p&H+%.#d0<DmLK*#-\8w:xD2Y[3jO{l8[)<(F[=Bcixb>Jp^%L2XvVTzW@9OTko/P74d1sFscEbMO7Vhp&HM;+ww/v[KM1%2M*7O\}rEZM.LM0'\iwK:])pg-nJef\Rt4-> base92:2WsR9eo=EA2%h#>&.;[@sVfC=]\cp;cldd<btVh:IeqR=))D<;Fjh`:3pGh9kmF$A6)#b;0kYf ...

在 pwn中，理解 ELF 文件的 PLT（Procedure Linkage Table，过程链接表）和 GOT（Global Offset Table，全局偏移表）是非常重要的。这些表格用于解决函数调用时的延迟绑定（Lazy Binding），并且与动态链接库加载和 ASLR（Address Space Layout Randomization）防御机制有密切的关系。 ELF 文件的延迟绑定机制 ELF 文件中，函数的调用通过 PLT 表和 GOT 表进行管理。延迟绑定意味着程序在第一次调用一个函数时，不直接解析其地址，而是通过一套机制将解析过程推迟到运行时。具体来说，ELF 文件利用 PLT 表与 GOT 表实现了这一机制。 PLT 表：每次调用动态链接库中的函数时，程序并不会直接跳转到目标函数的地址，而是先跳转到 PLT 表中相应的入口。PLT 表中的代码会跳转到 GOT 表对应项，若这是该函数第一次调用，则会通过动态链接器解析该函数的实际地址。 GOT 表：GOT 表中的每一项用于存储函数的实际地址。在函数第一次调用之前，该项保存的是指向 PLT 表的某个偏移量；在函数解析 ...

最近有亿点点焦虑，看到一句话“Life is too short to worry”，感到很受触动。一直以来，都在为着未来做打算，却忘了好好地活在当下。 作为一个闽南人，我非常喜欢这首闽南语歌曲《欢喜就好》： 人生海海 甘需要笼了解（人生很漫长，不需要每件事都清清楚楚） 有时仔清醒 有时轻睬（有时要很明白，有时就随意点） 有人讲好 一定有人讲歹（有人说好，一定有人说不好） 若唛想吓多 咱生活卡自在（如果不想太多，咱们的生活会很自在） 归工嫌车无够叭 嫌厝无够大（总嫌车不够拉风，嫌房子不够大） 嫌菜煮了无好吃 嫌某伤歹看（嫌菜做得不好吃，嫌老婆难看） 驶著好车惊人偷　大厝歹拚扫（开好车怕被偷，住大房难打扫） 食甲伤好惊血压高　媠某会缀人走（吃好太怕血压高，漂亮老婆会跟人跑了） 人生短短　好亲像咧七逃（人生短暂，就像是来游玩） 有时候烦恼 有时轻可（有时候烦恼，有时候轻松） 问我到底 腹内有啥法宝（问我到底肚子里有什么法宝） 其实无撇步，欢喜就好（其实没捷径，开心就好） 这句话和这首歌想表达的意思也许是相似的。人生短暂，没有太多时间去纠结于那些琐碎的烦恼和担忧，愿你能享受生活的每一 ...

省流版 以下是我把 项目方给的材料+我的每日总结+我的课堂笔记 喂给GPT生成的总结： 我非常荣幸能够在这个暑假参与卡内基梅隆大学（CMU）的"深度视觉与人工智能：探索视界未来"国际交流项目，这是一个独特的机会，让我深入了解了人工智能领域的前沿技术。该项目为期一个月，包括两周的线上预学习以及两周的线下课堂和文化体验。这次经历不仅让我提升了对深度学习和计算机视觉的认识，也让我有机会与来自全球的教授进行学术交流。 项目期间，课程内容涵盖了多个前沿主题，包括深度学习的基础理论、计算机视觉和3D视觉的最新研究进展。特别是Shubham Tulsiani教授的课程让我对3D视觉有了更深入的理解，学习了深度图、点云、网格等不同的表面表示方法，以及体素网格和隐函数等体积表示。课程还介绍了pinhole摄像机模型和齐次坐标等相关概念。我还学习了Retrival Augmented Generation (RAG) 模型和向量数据库的相关内容。RAG模型通过检索相关文档来增强生成式模型的回答能力，而向量数据库则在其中扮演了关键角色，能够进行嵌入的计算和比较。我们还学习了Hierarc ...

课程主页：https://courses.zjusec.com/ 课程简介 报名 这是一门短学期课程，报名需要提交一份Lab0实验报告或个人简历。提交Lab0的话只需要完成Prerequisite部分以及Misc, Reverse, Pwn, Web, Crypto部分五选一。但无论选择什么，上课之后最终都要把Lab0的五个方向做完，因为Lab0是课程的第一次作业，占5%。 授课教师 授课教师基本都是来自AAA的学长们，都非常牛而且人很好。 分数占比 考勤：5% Lab0：5% Lab1: 10% * 5 = 50% Lab2、Lab3: 10% * 2 * 2 = 40% 基本上每一个Lab都有Bonus，只能溢出到同一个周的Lab里。 学长们给分都很捞，再加上有Bonus，拿满还是不难的： 课程 课程时长共两周，第一周是导论部分，五个方向都需要上并完成相应的Lab1，第二周是专题部分，可以选择两个专题上课并完成这两个方向的Lab2、Lab3。 基本内容 课程分为Misc, Reverse, Pwn, Web, Crypto五个方向。 这是一门实操大于理论的课程，做的笔记参考价值 ...

问题 最近使用sing-box的TUN模式进行网络代理的时候遇到了一个坑。具体表现为，当设置"strict_route": false时，WSL网络正常，宿主机浏览器访问google.com却返回*.facebook.com的证书，经查发现这是经典的DNS污染。然而我设置的分流策略中google.com是走远程DNS的，理论上不应该出现这个问题： 12345678910111213141516171819202122232425"dns": { "servers": [ { "tag": "dns-direct", "address": "dhcp://auto", "detour": "out-direct" }, { "tag": " ...

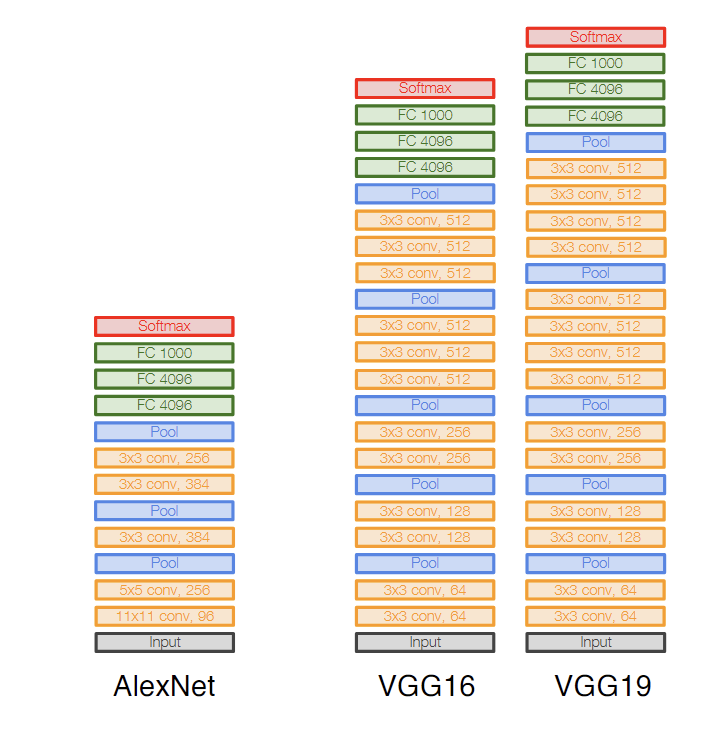
Lecture 8 AlexNet (2012) AlexNet是一个非常有影响力的卷积神经网络，Google Scholar显示，其原论文的引用已经达到了惊人的160203次。 AlexNet的结构就是(conv + [pool]) * 5 + (fc + dropout) * 3，随着层数的增加，图片的长宽不断减少，而通道数不断增多。当通道数达到一定数量时，它们会flatten后作为特征输入全连接神经网络中。 分析内存使用和参数量，可以发现AlexNet有趣的特征，随层数增加，内存占用变少，而参数量增多，即所有内存基本都在前面的卷积层，所有参数量基本都在后面的全连接层。 ZFNet (2013) ZFNet基本上就是一个更大的AlexNet，但是其基本结构依然是相同的，前面是卷积层和池化层，后面是全连接层。 VGG (2014) AlexNet和ZFNet的网络结构参数，即卷积核形状, 每层通道数，池化层形状，都是通过尝试人工设置出来的。这让网络的scale up变得困难。VGG提出了一种系统的卷积神经网络设计方法： 所有卷积层都是3x3, 步长为1, 填充为1：两个3x3的卷 ...

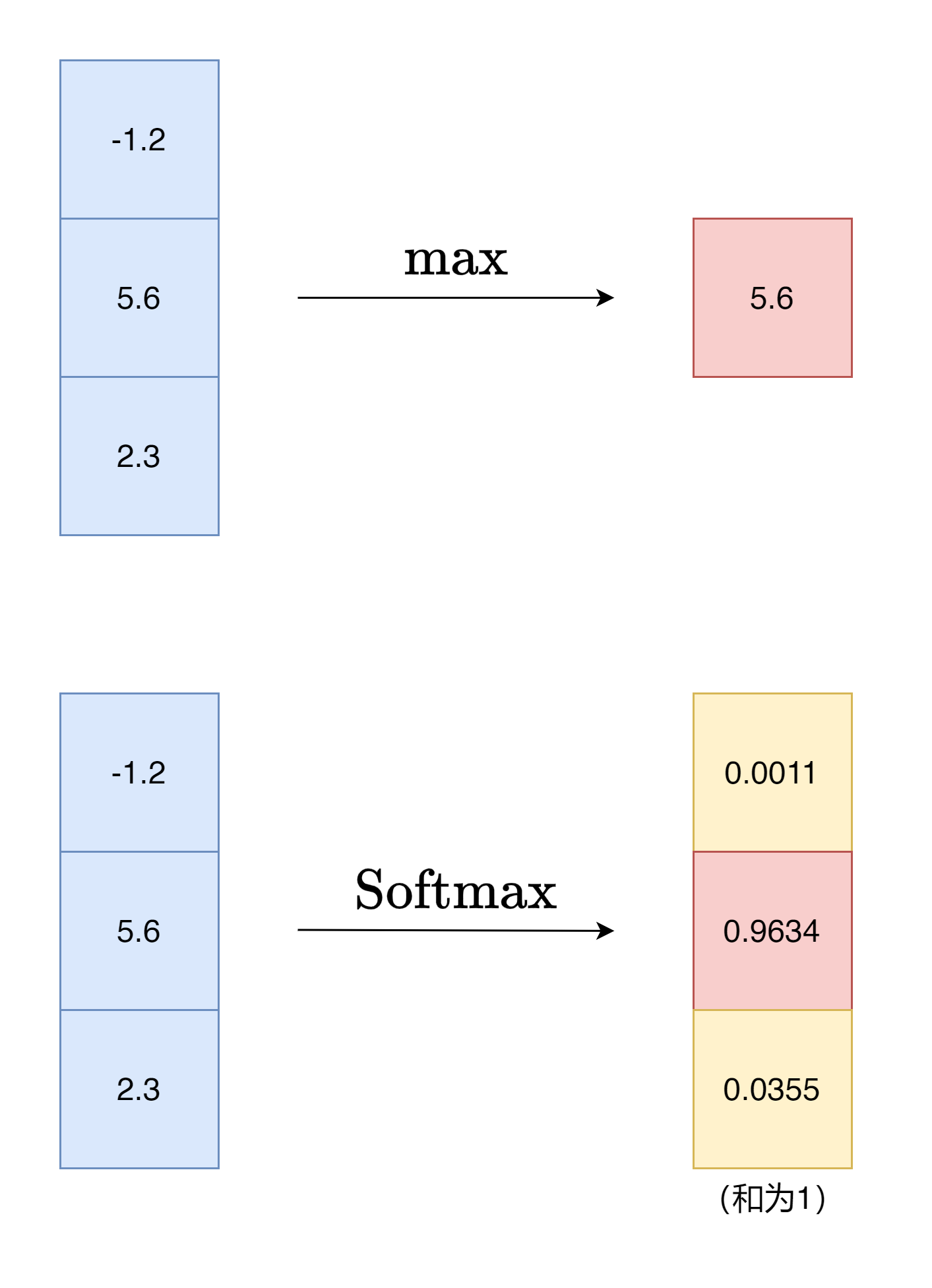
Softmax 是一种机器学习中常用的归一化函数。我们可以从它的名字来理解其含义。 Softmax 和普通的max 函数不同，它更加“软”，max 函数给出一组数据中唯一的最 大值，而Softmax 则会将向量归一化，归一化后的向量就可以视作一组概率分布，具 有实际意义。Softmax 中的指数的性质使输入中越大的数值对应越大的概率，并拉开 差距，让最大值显得更加突出。

FPGA流水线设计的策略 发现一篇非常好的讲FPGA中流水线设计的文章，搬运并翻译一下。 本文是https://zipcpu.com/blog/2017/08/14/strategies-for-pipelining.html的中文翻译。 学习FPGA的学生常常面临一个棘手的问题，FPGA中所有而事情都是并行发生的。 许多同学来自计算机科学专业，他们理解算法如何工作，一个操作需要在另一个操作之后顺序执行。他们很难理解算法中的每一步都对应着一块逻辑电路，需要在相应的时钟周期执行——无论是否使用。 解决操作顺序的一个方法是创建一个巨大的状态机。FPGA往往会同时创建所有状态的逻辑，并且仅在每个时周期结束的时候选择正确的答案。因此，状态机可以非常想我们讨论过的简单的多ALU（算术逻辑单元）。 另一方面，如果FPGA无论如何都会实现操作的所有逻辑，那么为什么不讲这些操作安排成一个序列，每个阶段都做一些有用的事情呢？这种方法将算法重新排列为流水线。流水线往往比状态机方法更快速完成相同的算法，甚至在资源利用方面有时也更高效，尽管这不一定。 数字逻辑流水线的难点在于，即使流水线的输入尚未有效，流水线 ...

线性空间到底是什么？ 我们在学习线性代数的时候，通常见到的线性空间是由以下八个条件共同定义的： 设KKK是一个数域，VVV是一个非空集合，同时还定义了： 向量加法：+:V×V→V+: V \times V \rightarrow V+:V×V→V 标量乘法：⋅:K×V→V\cdot: K \times V \rightarrow V⋅:K×V→V（⋅\cdot⋅也可省略） 且两种运算满足以下八条： 则成VVV是定义在KKK上的线性空间，又称向量空间。 向量加法单位元存在：存在θ∈K\theta \in Kθ∈K使得α+θ=α,α∈V\alpha + \theta = \alpha, \quad \alpha \in Vα+θ=α,α∈V，称θ\thetaθ为KKK的零元素，即向量加法的单位元。 向量加法逆元存在：存在∀α∈V,∃β∈V\forall \alpha \in V, \exists \beta \in V∀α∈V,∃β∈V使得α+β=θ\alpha + \beta = \thetaα+β=θ，称β\betaβ为VVV的负元素，即向量加法的逆元。 向量加法结合律：(α+β ...